Introdução
A estatística possui um grande papel na geração de energia elétrica e, por isso, merece um capítulo especial neste curso.
A demanda de energia, a água nas hidrelétricas, o sol na geração solar e os ventos, que acionam turbinas eólicas e provocam a dispersão de poluentes na atmosfera, e o preço dos combustíveis apresentam um comportamento randômico que só a estatística pode explicar.
Conceitos Básicos
Espaço de Amostragem
Espaço de amostragem – S - é o conjunto de todos os pontos de amostragem, definidos como sendo os possíveis resultados de um experimento ou sistema randômico.
Por exemplo, os conjuntos de todas as possíveis vazões de um rio, de todos os possíveis ventos em determinado ponto e de todos os possíveis preços de um combustível constituem espaços de amostragem.
Isto nos leva às seguintes questões práticas:
- É possível medi-lo?
- É possível determinar seus valores máximo e mínimo?
Os espaços de amostragem podem ser finitos, quando o número de pontos de amostragem é finito ou infinitos, quando o número de pontos de amostragem é infinito.
Eventos
Evento é um subconjunto A do espaço de amostragem S. Quando este subconjunto é unitário ele é chamado de evento elementar ou simples.
Por exemplo, as vazões medidas em determinado ponto de um rio nos últimos 80 anos, os ventos medidos em determinada localidade nos últimos 10 anos e o preço do petróleo nos últimos 5 anos são subconjuntos dos respectivos espaços de amostragem.
Probabilidade
No caso de Espaços de Amostragem finitos, se um evento – A - pode ocorrer de h maneiras diferentes de um total de n possibilidades diferentes e igualmente prováveis, sua probabilidade P(A) é definida como sendo h/n.
Por exemplo, a probabilidade de um determinado número entre 1 e 60 ser sorteado na megasena é igual a 1/60.
Portanto, definir a probabilidade de eventos bem definidos pertencentes a espaços de amostragem também bem definidos é simples.
No entanto, qual a probabilidade do preço do petróleo ultrapassar U$100/barril?
Para responder a esta pergunta, probabilidade também pode ser definida da seguinte maneira:
Se após n repetições de um experimento, onde n é um número suficientemente grande, um determinado evento A ocorreu h vezes, a probabilidade também é definida como sendo P(A)=h/n.
Matematicamente, pode-se definir a probabilidade como sendo:
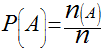
onde:
n(A) é o número de ocorrências do evento A;
n é o número total de eventos.
O grande problema desta definição é saber se n é grande o suficiente para garantir a precisão da probabilidade e, dado um n finito, qual o erro cometido.
Axiomas
- Para todo evento A, P(A)≥0, isto é, a probabilidade é sempre positiva.
- Para todo e qualquer evento A, 0≤P(A)≤1.
- P(A)=1 implica A é um evento certo.
- P(A)=0 implica que o evento A é impossível de ocorrer.
- Se o Evento A’ é o complemento de A, então P(A’)=1-P(A)
- Para quaisquer dois eventos A e B, a probabilidade da união dos dois eventos é dada por:
![]()
- Somatório ou integral das probabilidades de todos os eventos de um espaço S é igual a 1.
![]()
Probabilidade Condicional
Sejam A e B dois eventos de um espaço S com probabilidades maiores que zero. A probabilidade de B ocorrer dado que A ocorre é dada pela expressão abaixo.
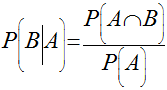
Lei de Bayes
Supondo A1, A2,....., An, eventos mutuamente exclusivos cuja união forma o espaço de amostragem S, isto é, um deles deve obrigatoriamente ocorrer a Lei de Bayes diz que:
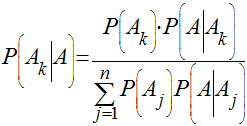
Eventos Independentes
Dois eventos são estatisticamente independentes se:
![]()
Três eventos são independentes se eles forem independentes dois a dois e se:
![]()
Análise Combinatória
A determinação do espaço de amostragem é fundamental para a análise estatística. Quando o espaço é finito e pequeno, a contagem direta é o caminho mais prático.
Contudo, existem espaços de amostragem que, mesmo sendo finitos, são, do ponto de vista prático, incontáveis.
Por exemplo, o espaço de amostragem do cara ou coroa é finito e pequeno. Por outro lado, o espaço de amostragem dos resultados da megasena, apesar de finito, é muito grande para uma contagem direta.
Árvore de Probabilidades
A árvore de probabilidades ou eventos é uma maneira de contagem direta do espaço de amostragem.
Exemplo
Todo dia o ONS tem de tomar a decisão de despachar as usinas térmicas ou não.
No entanto, se após esta decisão, as chuvas vierem em quantidades significativas, a decisão foi errada e teve um custo adicional de combustível desnecessário.
Por outro lado, se a decisão for não despachar as usinas térmicas e as chuvas não vierem nas quantidades necessárias, existe um risco de racionamento.
A Figura abaixo apresenta a árvore de probabilidades deste exemplo. A probabilidade de racionamento pode ser claculada como sendo o produto das probabilidades de não despachar as térmicas pela probabilidade de não chover.
A grande questão é como determinar a probabilidade de não chover a quantidade necessária.
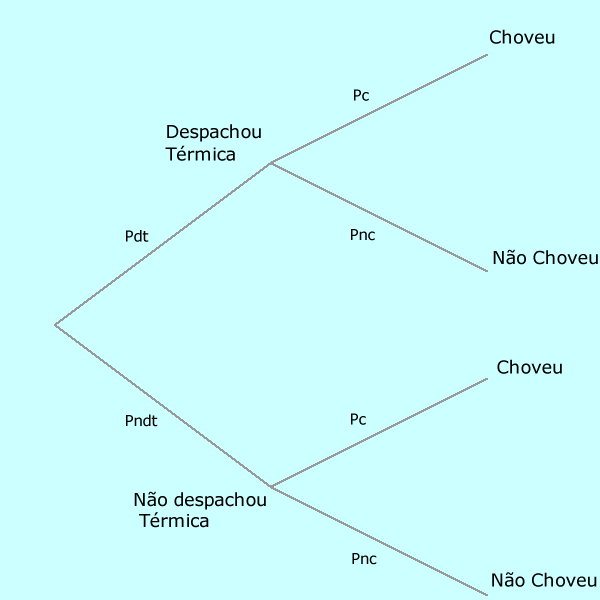
Árvore de probabilidades
Permutações
Suponha que existam n objetos distintos que desejamos arrumar r objetos deste conjunto em uma fila. Neste caso, existem n opções de se escolher o primeiro elemento, (n-1) opções de se escolher o segundo até (n-r+1) maneiras de se escolher o último objeto.
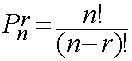
Combinações
No caso das permutações, a ordem dos objetos na fila é importante. Isto é, a fila abc é dirente da fila bca.
No entanto, isto nem sempre é o caso. Existem situações em que se deseja selecionar uma determinada quantidade de elementos sem se preocupar com a ordem.
Neste caso, teremos que:
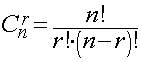
Função Probabilidade ou Distribuição de Probabilidade
Se associarmos um número a cada ponto de um espaço de amostragem, poderemos definir uma função: função randômica ou estocástica - f(x). Se o espaço de amostragem for finito as variáveis randômicas ou estocásticas serão discretas. Caso contrário, as variáveis são não discretas.
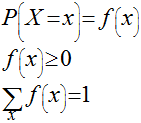
Função de Distribuição Acumulada ou Função de Distribuição
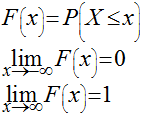
Valor Esperado ou Média
O valor esperado é um dos conceitos mais importantes da estatística. Ele representa o valor esperado ou mais provável de uma variável aleatória e é dado pelo somatório dos eventos ponderados pela suas respectivas probabildades, conforme a equação abaixo:
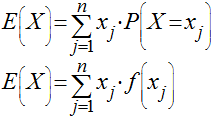
No caso das probabilidades serem iguais, o valor esperado é igual à média aritmética .
Quando isso não ocorre, dois outros conceitos são utilizados; a moda e a mediana.
Moda
A moda de uma variável randômica é o valor que ocorre com maior freqüência ou com maior probabilidade. Algumas vezes, existem variáveis randômicas com mais de um valor muito freqüente. Neste caso, a função de distribuição é chamada de bimodal ou multimodal.
Mediana
A mediana é o valor da variável randômica que separa a função de distribuição em duas metades iguais ou pode ser interpretada como sendo o valor com 50% de probabilidade de ocorrência.
Teoremas Sobre Valor Esperado
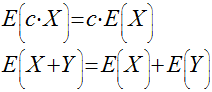
Se, e apenas se, X e Y forem variáveis randômicas independentes, teremos que:
![]()
Variância e Desvio Padrão
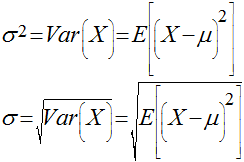
Teoremas Sobre Variância
![]()
Se, e somente se, X e Y forem variáveis randômicas independentes, teremos que:
Momento de Ordem r
O momento de ordem r é definido como sendo o valor esperado dos desvios elevados a r.
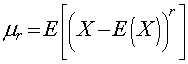
Existem casos especiais de momentos que fornecem informações importantes sobre as variáveis randômicas.
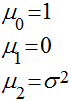
Distorção (Skewness)
A distorção mede o grau de assimetria da distribuição de uma variável aleatória em relação ao valor esperado e é definida como sendo:
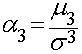
A Distorção pode ser positiva ou negativa conforme a distorção seja para a direita ou esquerda respectivamente. Distorção igual a zero significa uma distribuição perfeitamente simétrica em relação ao valor esperado, como a distribuição normal.
Curtose (Kurtosis)
A curtose mede o quanto a distribuição da variável aleatória é mais plana ou não e é dada por:
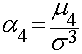
Valores maiores do que 3, que é o valor da distribuição normal, representam distribuições com picos elevados e valores menores do que 3 representam distribuições mais planas ou achatadas.
Normalização de Variáveis Aleatórias
Dada uma variável aleatória com média μ e desvio padrão σ, a variável pode ser transformada em uma variável aleatória estandardizada da seguinte maneira:
![]()
Covariância
Considerando duas variáveis aleatórias X e Y com função densidade de probabilidade igual a f(x,y), teremos que:
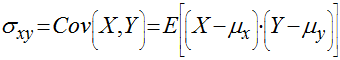
Se X e Y são variáveis randômicas independentes, a covariância é igual a zero.
Fator de Correlação
Portanto, o fator de correlação entre duas variáveis aleatórias é dado por:
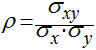
O fator de correlação varia entre -1, negativamente correlacionado e 1, positivamente correlacionado. Um fator de correlação zero significa que as variáveis são independentes.
Funções de Distribuição
Distribuição de Binomial
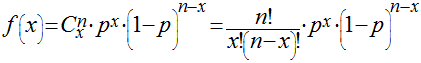
Esta distribuição representa a probabilidade de um evento, com probabilidade p de ocorrer e q (igual a 1-p) de não ocorrer, ocorrer x vezes em n tentativas. No caso especial de n=1, esta distribuição se transforma na Distribuição de Bernoulli. Esta Figura mostra a função da probabilidade Binomial. A média, variância, distorção e curtose são dados abaixo.
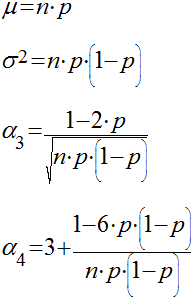
Distribuição Normal ou Gaussiana
A distribuição normal é uma das distribuições mais conhecidas e utilizadas.
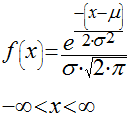
Distribuição Lognormal
Na prática, muitas distribuições de probabilidade possuem inclinação devido a leis da física que governam o tipo de evento analisado. Diversos fenômenos físicos, tais como vento, precipitação e vazão, não possuem valores negativos mas não possuem limitações superiores. Isto faz com a distribuição estatística dessas grandezas apresente uma inclinação para a direita e, por isso, não podem ser aproximados pela distribuição normal. No entanto, o logaritmo dessas grandezas pode ser aproximado pela distribuição normal. Daí resulta a Distribuição Lognormal.
Distribuição de Gumbel
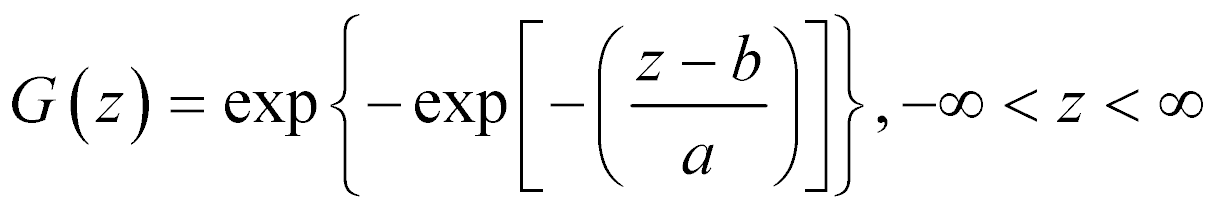
Distribuição de Fréchet
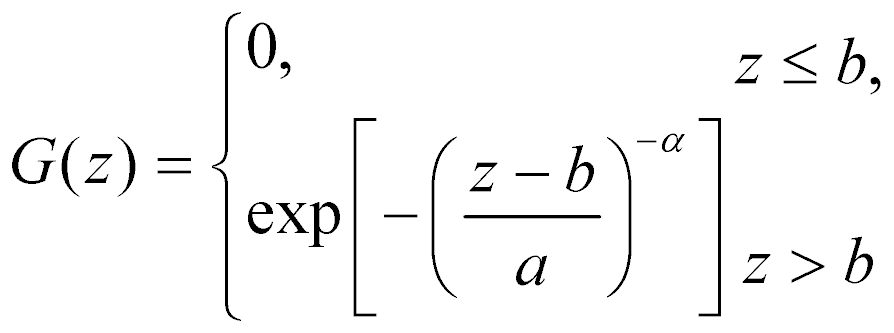
Distribuição de Weibull
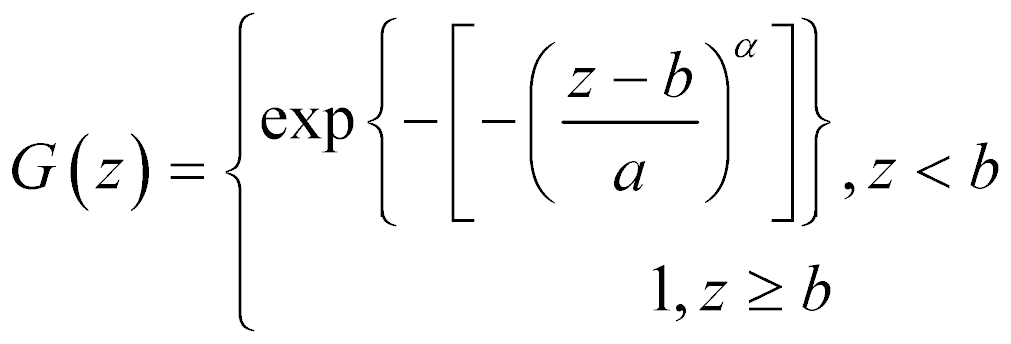
Histogramas
O Histograma é a forma de se obter, a partir de um conjunto de dados, a distribuição estatística desta amostra.