Introdução
A mecânica dos fluidos é fundamental no estudo da geração de energia elétrica.
Todas as máquinas térmicas e hidráulicas obedecem às leis da mecânica dos fluidos assim como todas as fontes primárias de energia, que podem ser analisadas como fluidos.
A teoria foi desenvolvida de duas maneiras: diferencial e integral.
A base diferencial considera o fluido pontualmente no espaço enquanto o tratamento integral considera um volume.
Ambas as maneiras são corretas e a escolha de qual utilizar depende da aplicação prática em estudo.
Sistemas de Coordenadas
Todo ponto no espaço pode ser representado por um sistema de coordenadas tridimensional.
Dois sistemas são utilizados na geração de energia:
- Cartesiano;
- Cilíndrico Polar;
Sistema Cartesiano
O sistema mais usual e simples de entender é o sistema retangular Cartesiano, representado na figura abaixo.

Neste sistema, os operadores matemáticos Gradiente, Divergente e Rotacional das grandezas escalar V e vetorial F serão dados por:
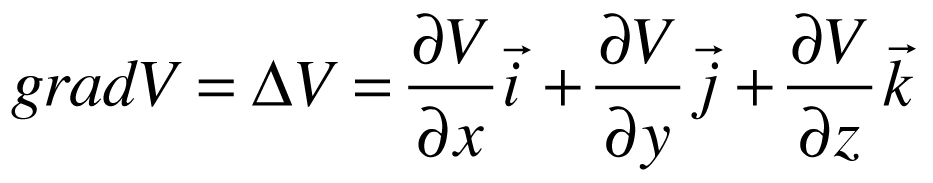
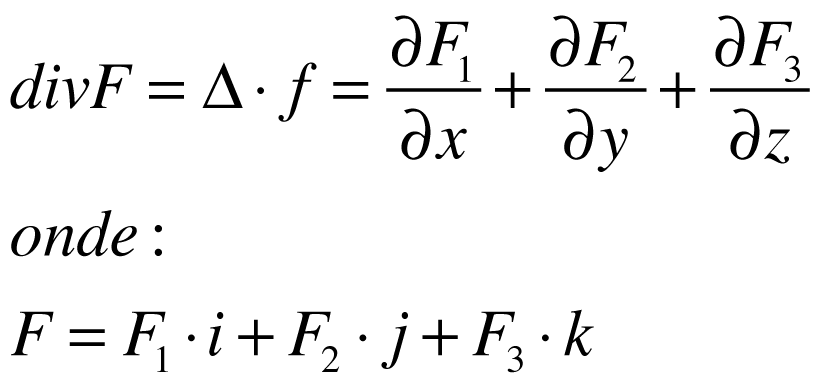
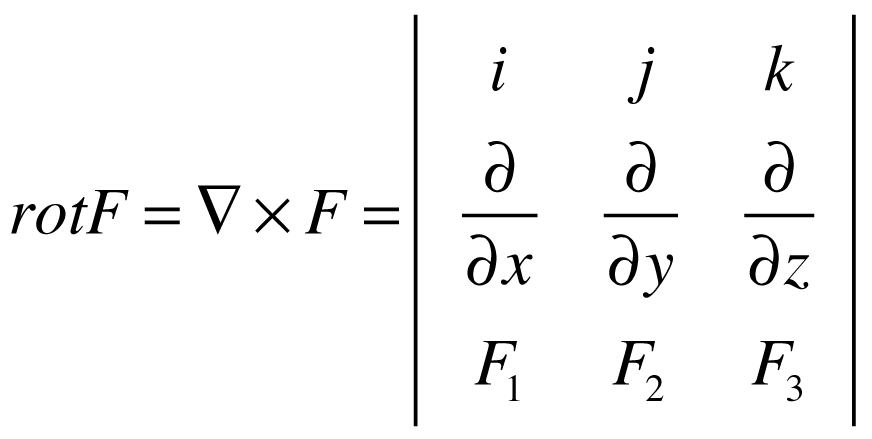
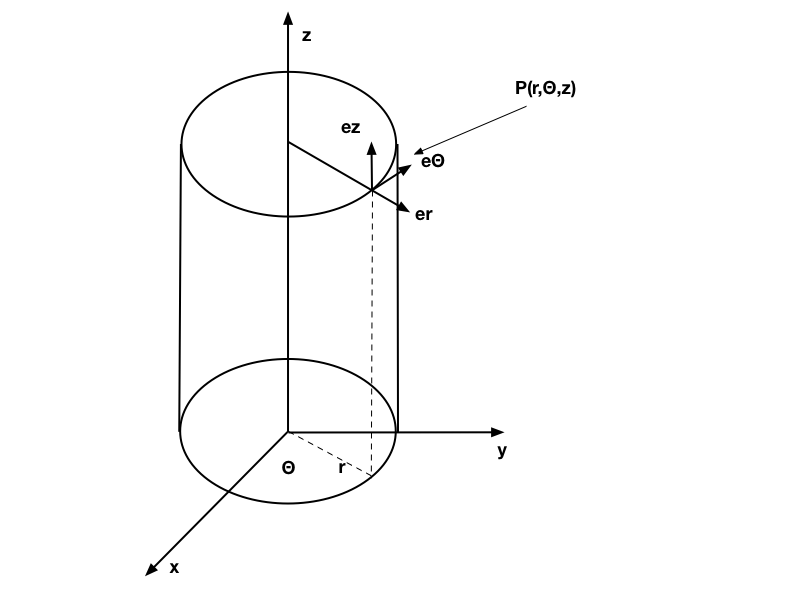
Sistema Cilíndrico Polar
Como a maioria das máquinas utilizadas na geração de energia giram e são cilíndricas, o sistema cilíndrico polar é muito utilizado.
Este sistema é apresentado na figura abaixo. Neste caso, o eixo dos x é transformado no raio e o eixo dos y no ângulo formado entre o eixo dos x e o eixo dos y. O eixo z permanece inalterado.
A relação entre os dois sistemas de coordenadas é:
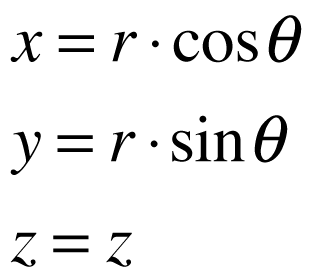
Neste sistema, os operadores matemáticos Gradiente, Divergente, Rotacional e Laplaciano de grandeza escalar V e vetorial F serão dados por:
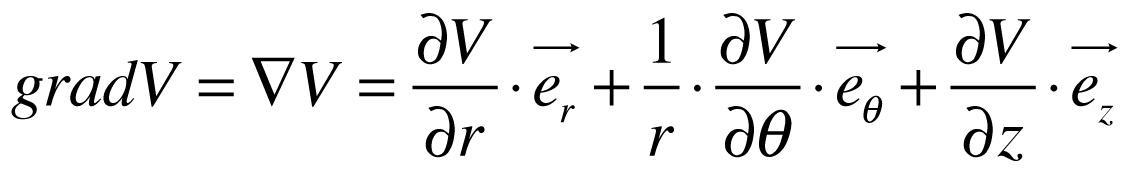
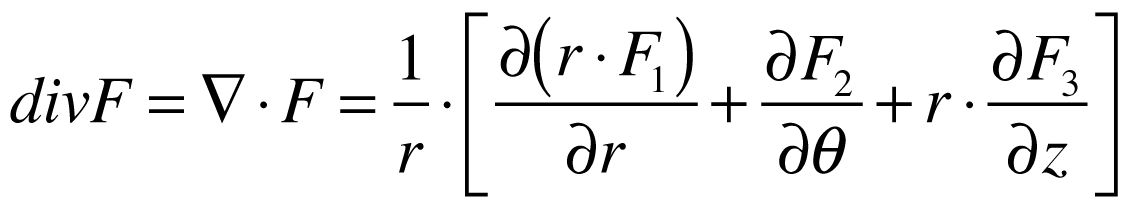
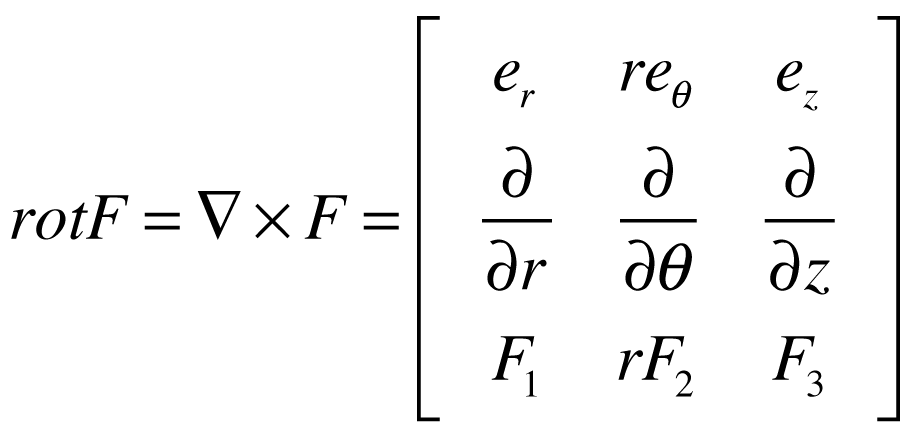
Cinemática dos Fluidos
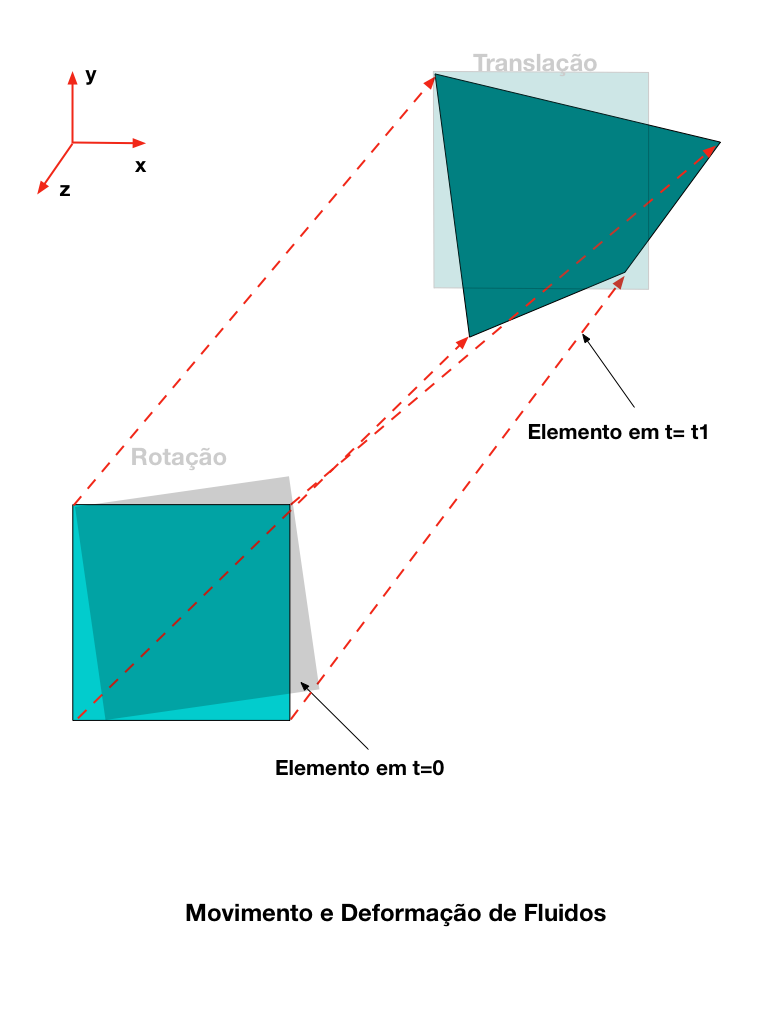
A figura abaixo mostra o movimento de uma partícula elementar ou volume de fluido entre o instante 0 e o instante t1.
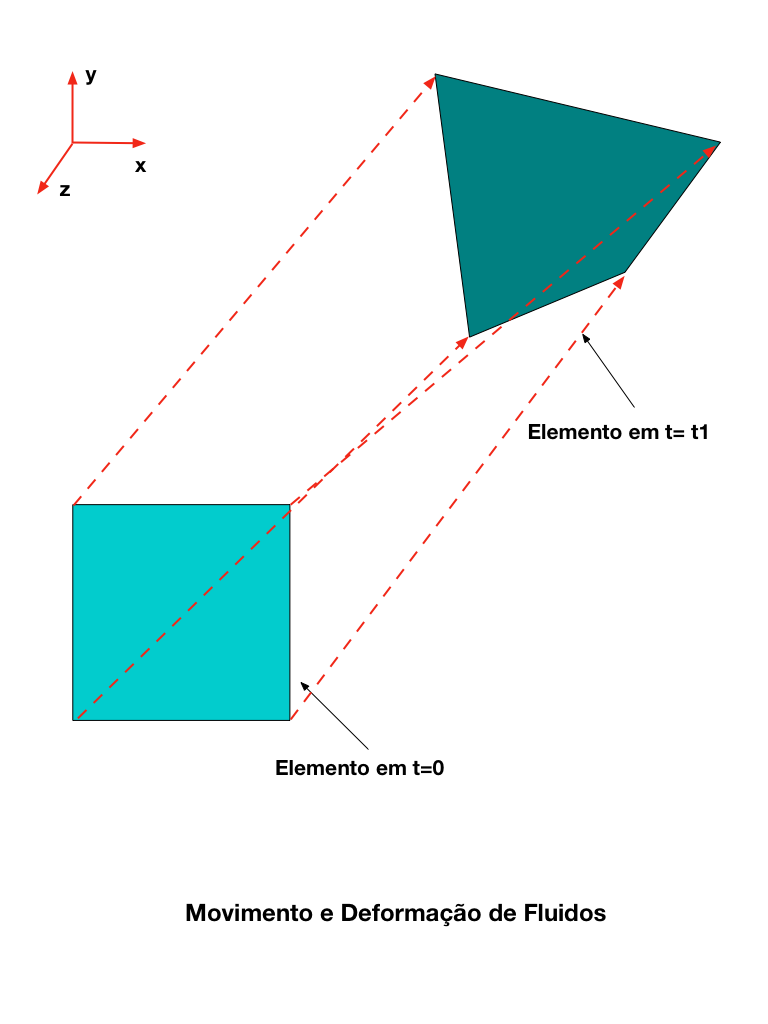
De uma forma geral, este movimento pode ser decomposto nos seguintes movimentos básicos:
- Translação;
- Deformação linear;
- Rotação;
- Deformação angular.
Portanto, a velocidade de determinado ponto do fluido é dada por:
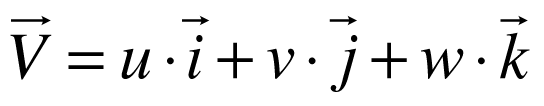
Linhas de fluxo são linhas imaginárias traçadas como tangentes ao vetor de velocidade ao longo do tempo e espaço. Se o fluxo estiver estável e estacionário, as linhas de fluxo são fixas no espaço.
A aceleração de uma partícula do fluido é dada por:
Viscosidade
A densidade e o peso específico são medidas do "peso" de um fluido e não são suficientes para descrever totalmente seu comportamento.
Água e óleo possuem aproximadamente a mesma densidade mas apresentam comportamento distinto com relação ao escoamento.
Intuitivamente, fluidos tendem a grudar nas superfícies sólidas que os contem, mesmo quando estão em movimento.
Esta característica "pegajosa" dos fluídos é denominada de viscosidade.
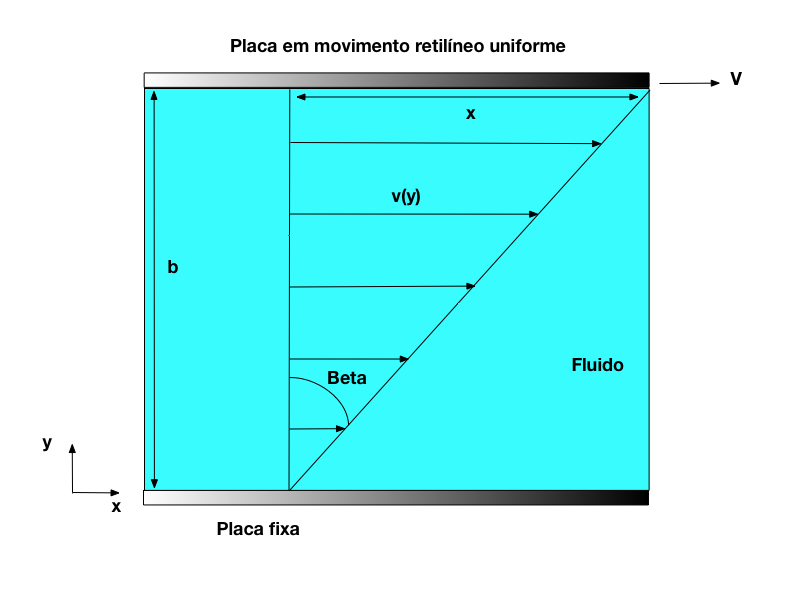
A figura abaixo utiliza experimento ideal para quantificar esta propriedade.
Supondo um fluido entre duas placas paralelas, uma parada e outra se deslocando linearmente com velocidade constante V, a velocidade do fluido apresentará um perfil de variação linear.
Como o fluido "gruda" nas superfície sólidas, a velocidade do fluido em contato com as placas será igual à velocidade da placa.
Para um grande número de fluidos, a variação da velocidade entre as placas é linear e pode ser escrita da seguinte maneira:
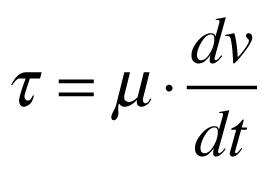
Onde:
- μ é a viscosidade absoluta, viscosidade dinâmica ou apenas viscosidade;
- τ é a tensão de cizalhamento;
- v é a velocidade
Equação de Bernoulli
A equação de Daniel Bernoulli (1700 a 1782) estabelece que, para fluidos incompressíveis, sem realização de trabalho e sem transferência de calor a energia total será constante conforme a expressão abaixo:
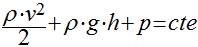
Onde:
v é a velocidade;
ρ é a densidade do fluido;
g é a aceleração da gravidade;
h é a altura com relação a um referencial;
p é a pressão.
As premissas para o uso desta equação são:
- Fluido sem viscosidade;
- Escoamento estacionário;
- Fluido incompressível;
Esta expressão também é escrita de outras formas, dividindo-se todos os termos pelo peso específico do fluído ou por sua densidade.
Todas são equivalentes e a vantagem de uma em relação à outra depende do tipo de problema analisado.
Densidade do Ar