Apesar de apresentar algumas falhas, a teoria de Drude permaneceu como a base teórica para a resistividade e condutividade durante 27 anos. Somente a partir da Mecânica Quântica as falhas do modelo de Drude foram solucionadas. Por exemplo, a relação entre a Capacidade Térmica dos metais e a corrente elétrica apresentava discrepâncias no modelo de Drude.
As discrepâncias do Modelo de Drude resultam da hipótese de considerar o comportamento dos Elétrons semelhante ao comportamento das moléculas dos gases.
Somente a partir de 1926, com a introdução da distribuição estatística de Fermi-Dirac para explicar o comportamento dos Elétrons no lugar da distribuição de Maxwell-Boltzmann, que explica os gases, a teoria da Condutividade e Resistividade evoluiu.
Em 1927, Sommerfeld utilizou a distribuição de Fermi-Dirac para descrever o mecanismo de condução de corrente nos metais.
Este novo modelo, denominado de Drude-Sommerfeld permitiu explicar o relacionamento entre condutividade elétrica e térmica e o coeficiente Seeback do Efeito termoelétrico.
A Equação 1 apresenta a distribuição de probabilidade de Maxwell-Boltzmann utilizada por Drude, e a Equação 3 mostra a distribuição de Fermi-Dirac utilizada por Sommerfield para determinar a probabilidade da velocidade dos Elétrons.
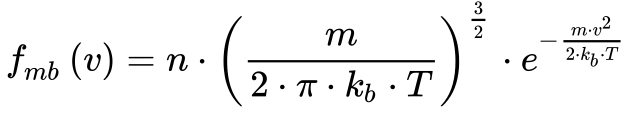
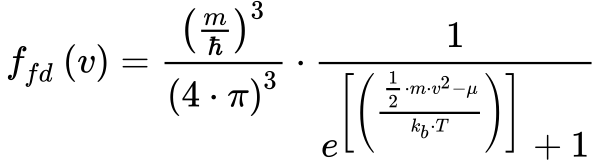
Onde:
-
- n é a densidade dos Elétrons;
- m é a massa do Elétron;
- kb é a constante de Boltzmann;
- T á a temperatura [K];
- v é a velocidade do Elétron;
- h cortado é a constante de Planck dividida por 2π;
