Matemática Financeira

“Finanças consiste na arte de passar dinheiro de mão em mão até ele desaparecer”

Robert Sarnoff, foi Presidente da RCA

Independentemente da profissão, a matemática financeira se tornou indispensável à vida cotidiana. O milionário a utiliza para preservar sua fortuna, e todos devem aplicá-la para construir seu patrimônio.

Por razões obscuras, seu ensino se encontra restrito aos cursos relacionados à área financeira, apesar de ser indispensável na engenharia.

Os engenheiros necessitam conhecê-la para criar soluções economicamente viáveis, de modo que as empresas possam pagar seus salários.

Índice

1. Tempo é dinheiro
2. Valor Futuro
3. Valor Presente
4. Pagamentos Constantes
5. Amortizações Constantes
6. Inflação
7. Viabilidade de Projetos
   1. Valor Presente Líquido
   2. Taxa Interna de Retorno
   3. Tempo de Retorno

 

Tempo é Dinheiro

Tempo é dinheiro, mas como medi-lo?

A variação do valor econômico das coisas¹ com o tempo constitui a base da matemática financeira. A Figura 1 apresenta o conceito de valor futuro. Quanto maior o tempo, maior a mudança do valor futuro, que pode ser positiva ou negativa. Mas, como medir a velocidade desta variação?

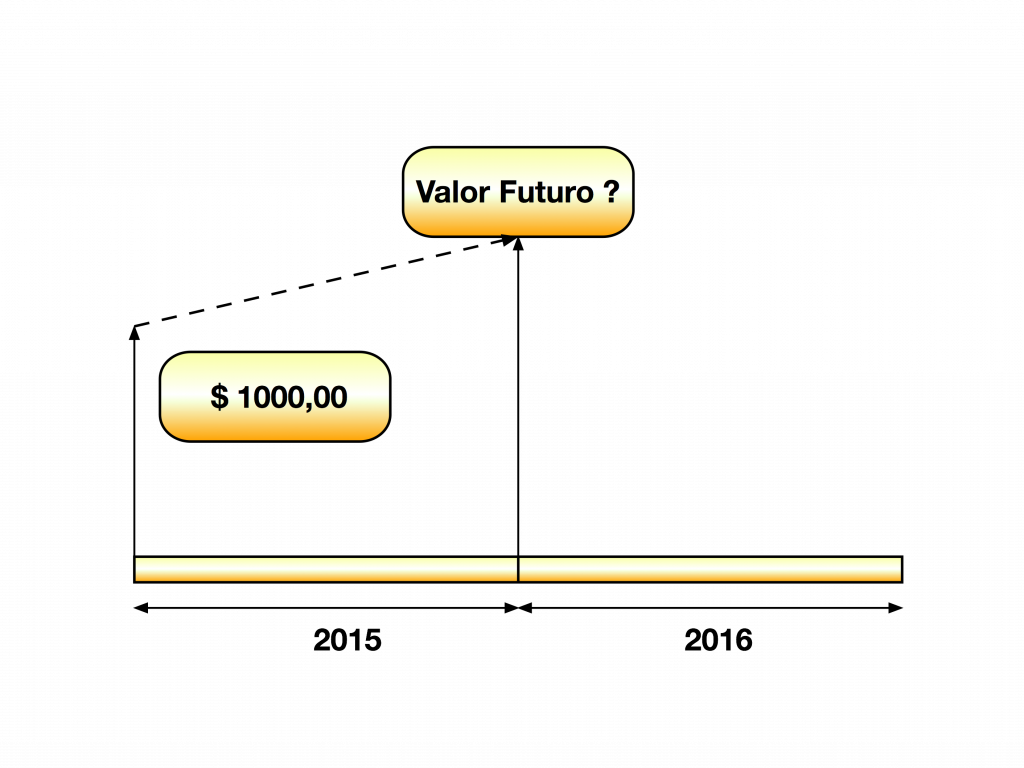
A velocidade da variação de valor pode ser expressa em $/ano ou em $/mês, onde $ representa qualquer unidade monetária². No entanto, esta velocidade possui um valor relativo diferente dependendo da comparação ser feita com o valor inicial ou final.

Por isso, normaliza-se esta velocidade tendo como base o valor existente no instante inicial. A escolha do ponto inicial depende da situação específica e não precisa necessariamente ser o momento presente. ³ Por exemplo, considerando a Figura 1, se a velocidade da variação de valor fosse de R$100,00 por ano, a velocidade normalizada seria de 10% ao ano. Portanto, o conceito de velocidade de variação de valor também depende da unidade de tempo considerada.

Utilizando este conceito, o valor futuro equivale ao valor inicial mais o incremento relativo à velocidade de variação.

Denomina-se a velocidade de crescimento de valor de taxa de desconto. Em operações financeiras, denomina-se esta taxa de taxa de juros. Juros existem apenas em operações de empréstimo, para investimentos denominamos esta velocidade de taxa de retorno. Por isso, utilizaremos a denominação de taxa de desconto para designar juros ou taxa de retorno indistintamente no desenvolvimento dos conceitos de matemática financeira. A matemática financeira independe da nomenclatura, mas a escolha correta da taxa na resolução de questões práticas requer experiência e compreensão do problema específico.

Índice

Valor Futuro

O Valor Futuro da Figura 1 é igual ao valor presente mais o aumento provocado pela taxa de desconto conforme a equação abaixo:

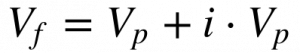
Onde:

• • V_f é o valor futuro;
  • V_p é o valor presente;
  • i é a taxa de desconto.

---

Exemplos

1. Você emprestou R$ 100 e recebeu R$ 110 no mês seguinte. Qual a taxa de desconto desta operação? Qual a taxa de retorno e qual a taxa de juros? ⁴

2. Você emprestou R$ 100 e recebeu R$ 90 depois de 1 ano. Qual a taxa de juros deste empréstimo? ⁵

3. Você emprestou R$ 100 e recebeu R$ R$101 no dia seguinte. Qual a taxa de juros deste empréstimo? ⁶

4. Qual a maior taxa de juros dos exemplos anteriores? ⁷

---

Quando a frequência de capitalização da taxa de desconto é diferente da base de tempo do fluxo financeiro, surge a questão da capitalização da taxa de desconto. A Figura 2 mostra este conceito.

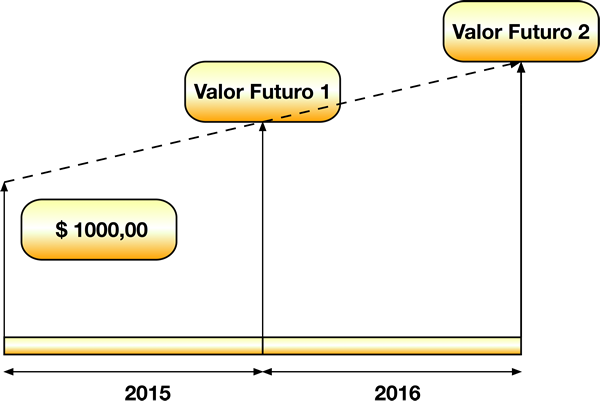
Considerando a taxa de desconto constante⁸, calcula-se o valor futuro 2 a partir da equação 1 da seguinte maneira:

Analogamente, escreve-se o valor futuro no período n da seguinte maneira:

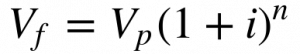
Onde:

• • n é um número inteiro que representa o período futuro.

Calcula-se a quantidade total de juros paga de acordo com a equação abaixo:

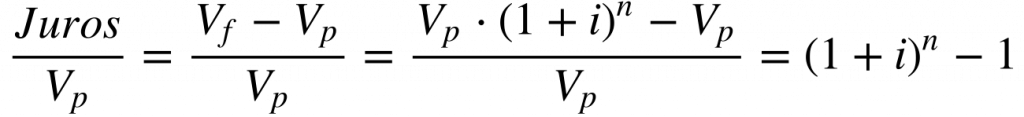
Observa-se que os juros crescem exponencialmente com o número de períodos de capitalização.

A quantidade de juros depende da frequência de capitalização. Na prática, o mercado utiliza frequências de capitalização mensais, trimestrais, semestrais e anuais. Países com taxas de juros ou inflação elevadas empregam frequências de capitalização mensal, enquanto economias estáveis operam com frequências semestrais ou anuais. O ajuste da frequência de capitalização afeta a taxa de desconto real e o cálculo do valor futuro da seguinte maneira:

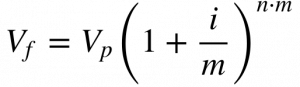
Onde:

• • m é a frequência de capitalização por ano;
  • n é o número de anos;
  • i é a taxa de desconto nominal anual.

Normalmente, anunciam-se as taxas como um percentual ao ano – % a.a. Porém, essa informação encontra-se incompleta porque não expressa a frequência de capitalização.  

A equação 5 mostra como ajustar as taxas anuais de acordo com a frequência de capitalização.

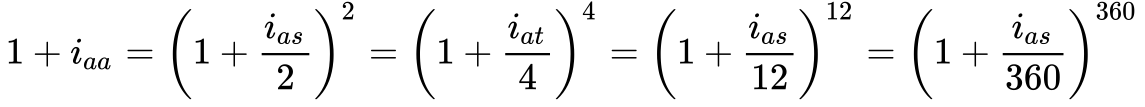
Onde:

• • i% _a.a  é a taxa anual capitalizada anualmente;
  • i% _a.s é a taxa anual capitalizada semestralmente;
  • i% _a.m é a taxa anual capitalizada mensalmente;
  • i% _a.d é a taxa anual capitalizada diariamente.

Em decorrência das elevadas taxas de juros e/ou inflação, as taxas de juros capitalizadas mensalmente podem ser expressas ao mês. Quanto isto ocorre, deve-se utilizar as equações abaixo:

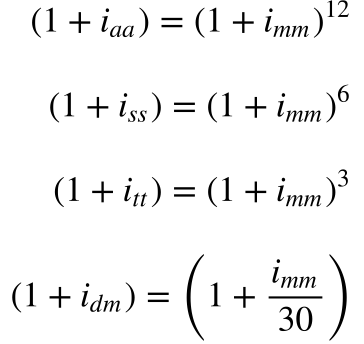
Onde:

• • i_aa é a taxa de desconto anual capitalizada anualmente;
  • i_mm é a taxa de desconto mensal capitalizada mensalmente;
  • i_ss é a taxa de desconto semestral capitalizada semestralmente;
  • i_tt é a taxa de desconto trimestral capitalizada trimestralmente;
  • i_dm é a taxa de desconto diária capitalizada mensalmente;

Como o tempo existe de forma contínua, a capitalização dos juros também pode ocorrer continuamente.  A partir da equação 4 , calcula-se a taxa de desconto com capitalização contínua da seguinte maneira:

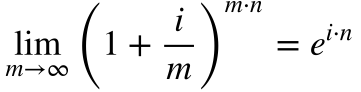
Por exemplo, uma taxa de desconto de 12% ao ano capitalizada mensalmente equivale, baseado na equação 5, a 12,68 % aa. Porém, se a capitalização fosse contínua, esta taxa passaria para 12,74% de acordo com a equação 7.

---

Exemplos

5. Qual a capitalização do exemplo 1? ⁹

6. Qual a capitalização do exemplo 3? ¹⁰

7. Qual a taxa de desconto do exemplo 3 em base mensal? ¹¹

Índice

---

Valor Presente

Calcula-se o valor presente a partir da equação 2 da seguinte maneira:

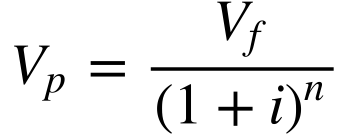
Dependendo do caso, calcula-se o valor presente a partir da equação 4.

---

Exemplos

8. Qual o valor futuro de $ 1 000,00 depois de 6 meses com uma taxa de 1% a.m capitalizada mensalmente? ¹²

9. Qual o valor presente de $ 1 000,00 daqui a 6 meses com uma taxa de 1% a.m capitalizada mensalmente? ¹³

Índice

---

Sistema de Pagamentos Constantes

O sistema de prestações, pagamentos, ou recebimentos periódicos acontece frequentemente e denomina-se Tabela Price. Neste sistema, conforme mostra a Figura 3, pagamentos iguais ocorrem com periodicidade constante durante n períodos.

Como calcular o valor futuro e o valor presente deste sistema de maneira mais simples do que pela aplicação direta das equações 2 e 8?

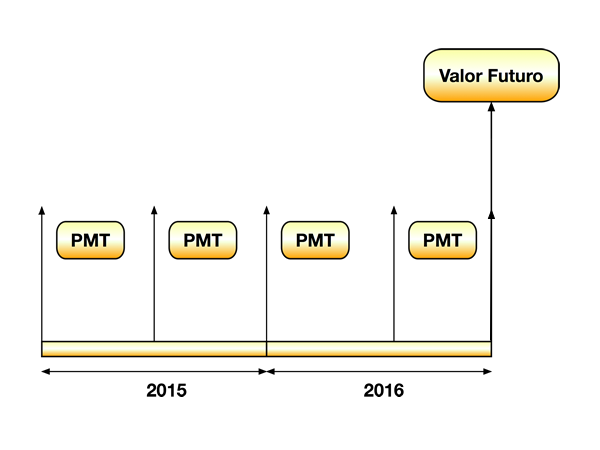
Utilizando a equação 2, calcula-se o valor futuro deste fluxo financeiro através da seguinte série:

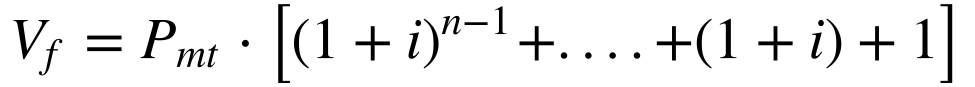
Onde:

• • P_mt é o pagamento ou recebimento constante. ¹⁴

Multiplicando ambos os lados da equação por (1+i), teremos que:

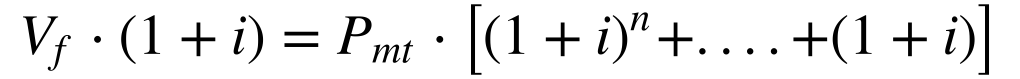
Subtraindo a equação 10 da equação 9, obtemos:

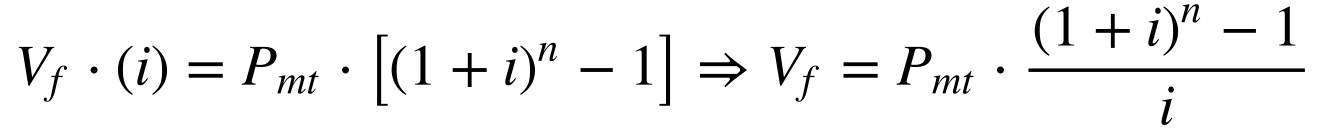
Por sua vez, calcula-se o valor presente, aplicando a equação 8 na equação 11 da seguinte maneira:

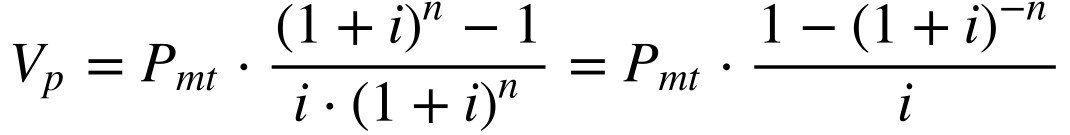
Esta equação possui quatro variáveis; V_p, P_mt, i e n, e deve-se conhecer três delas para calcular o valor da restante.

Quando se conhece a taxa de desconto (i) e o número de períodos (n), basta aplicar diretamente a equação 12 para calcular uma das outras duas variáveis (V_p ou P_mt).

Contudo, quando número de período se torna incógnita, precisamos manipular algebricamente a equação para achar a solução analítica. Para isso, aplicamos a seguinte mudança de variáveis:

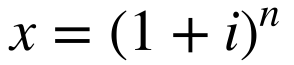
Substituindo esta nova variável na equação 10, teremos que:

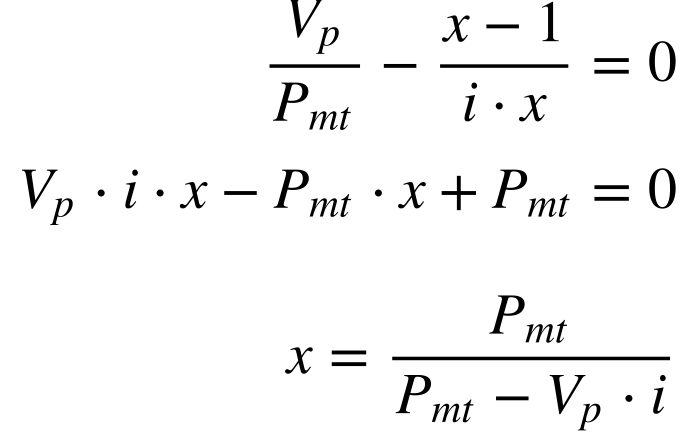
Substituindo a equação 13 na equação 14, teremos que:

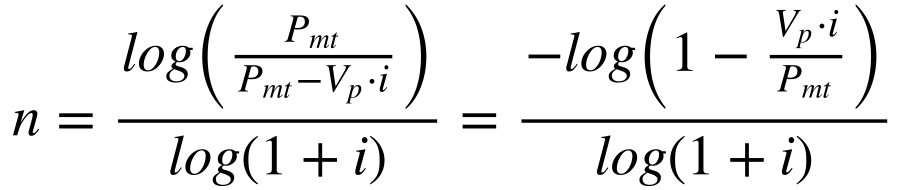
A partir desta equação, observa-se que o valor do pagamento periódico (P_mt) deve ser maior que o valor presente multiplicado pela taxa i (V_p.i) para que exista solução. ¹⁵ Em outras palavras, V_pi/P_mt deve ser menor do que 1.

Finalmente, para calcular o valor de i, manipulamos a equação 12 e criamos a seguinte função:

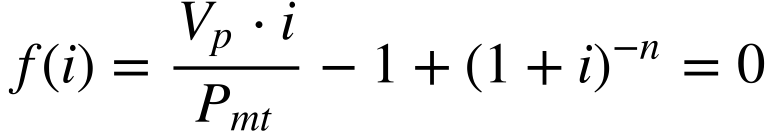
Esta equação não possui solução analítica, mas a disponibilidade de calculadoras e planilhas eletrônicas permite resolver este problema rapidamente utilizando técnicas numéricas de solução de equações não lineares. ¹⁶

A Figura 4 apresenta o valor presente normalizado com relação ao pagamento¹⁷ para diversos valores de i e n.

Observa-se que o valor presente dividido pelo pagamento diminui com o aumento do número de prestações e com aumento da taxa de juros. Além disso, ele converge para o valor de 1/i quando o número de períodos tende a infinito. ¹⁸ Este valor, denominado perpetuidade, representa o valor presente de um pagamento perpétuo com taxa i.

Por outro lado, o valor presente tende a zero quando a taxa i tende a infinito, demonstrando que quanto maior a taxa, menos valem as receitas futuras.

Além disso, a Figura 4 permite resolver a equação 16 graficamente. Determina-se a taxa i pela interseção da reta paralela ao eixo i no valor de V_p/P_mt  com a curva do número de períodos desejado.

[em manutenção]

Figura 4. Valor presente normalizado da Tabela Price

Calcula-se o total de juros pagos neste sistema da seguinte maneira:

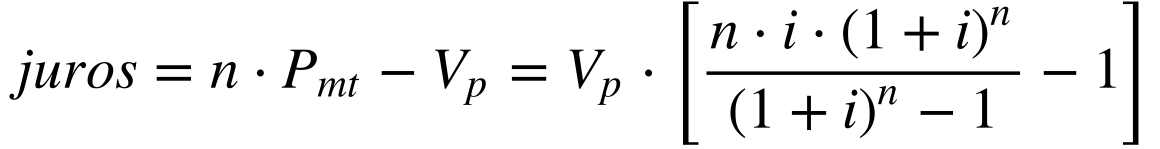
Observa-se que o total de juros pagos cresce exponencialmente com o número de períodos. Por isso, deve-se evitar financiamentos de longo prazo com este tipo de pagamento.

---

Exemplos

10. Considere uma compra de $ 1 000 parcelada em 5 vezes iguais com juros de 1% ao mês com capitalização mensal. Determine o valor da prestação e o total de juros pagos. ¹⁹

Tabela Price

Tabela 1 - Capital $ 1 000,00 e juros 1% a.m

Mês	Saldo Devedor Inicio mês	Pagamento	Amortização	Juros	Saldo devedor Final mês
0	$1 000,00	-	-	$10,00	$1 010,00
1	$1 010,00	$206,04	$196,00	$8,04	$812,00
2	$812,00	$206,04	$197,96	$6,06	$612,02
3	$612,02	$206,04	$199,98	$4,06	$410,04
4	$410,04	$206,04	$201,98	$2,04	$206,04
5	$206,04	$206,04	$204,00	-	-
Total	-	$1030,2	$1000	$30,2	-

11. Seu cartão de crédito propôs financiar um saldo devedor de $ 1 000,00 em 24 prestações mensais de $ 99,84. Determine a taxa de juros mensais e capitalização mensal cobrada. ²⁰

12. Qual a taxa de juros equivalente que seu cartão cobra ao ano com capitalização anual? ²¹

13. Determinada loja oferece um produto em 10 parcelas mensais de R$ 500,00 no carnê sem juros. É melhor comprar com o financiamento do cartão de crédito do exemplo anterior ou diretamente pela loja? ²²

14. Considerando que você possui R$ 5.000,00 aplicados na caderneta de poupança rendendo 0,5% ao mês com capitalização mensal, calcule o menor desconto que você deve aceitar para comprar o produto do exemplo anterior à vista. ²³

15. Considerando que a taxa de lucro da loja é de 20% ao ano, determine o maior desconto que o comerciante deve aceitar para vender o produto à vista. ²⁴

16. Por que o maior desconto aceitável pelo comerciante é maior do que o menor desconto aceitável pelo comprador? Resposta: a taxa de lucro da loja é maior do que a taxa do rendimento da poupança do consumidor. ²⁵

17. Estime o valor presente de $ 100,00 depositados mensalmente numa aplicação que rende 10% ao ano com capitalização mensal. ²⁶

---

Índice

Sistema de Amortizações Constantes

Utiliza-se o sistema de prestações constantes em operações financeiras para o consumidor e financiamento de bens de consumo de valores reduzidos devido ao valor constante das prestações.

Em operações de alto valor e longo prazo ²⁷ utiliza-se o sistema de amortizações constantes – sistema SAC, conforme a Tabela 2.

Observa-se que as prestações mensais decrescem, mas os pagamentos iniciais são maiores do que os pagamentos do sistema de pagamentos constantes. Contudo, o total de juros pagos é menor. Por isso, este sistema de pagamento tornou-se o preferido em empréstimos de longo prazo.

A amortização se resume ao valor presente dividido pelo número de pagamentos e os juros são dados por:

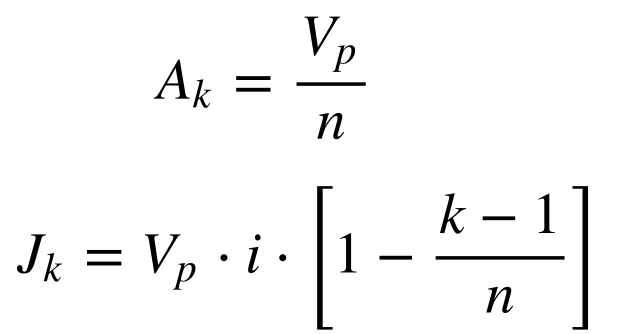
Onde:

• • A_k é a amortização no período de tempo k;
  • V_p é o valor presente;
  • n é o número total de períodos de tempo;
  • i é a taxa de juros ou retorno;
  • k é um dos períodos de tempo.

A Equação 19 fornece o valor total de juros pagos pelo sistema SAC.

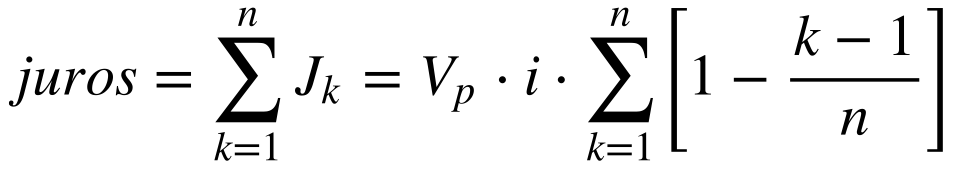
Comparando as tabelas 1 e 2, observa-se que o total de juros pagos é menor, mas os pagamentos durante a primeira metade do financiamento são maiores do que o financiamento com a Tabela Price.

Sistema SAC

Tabela 2 - Capital $ 1 000,00 e taxa de juros de 1% a.m

Mês	Saldo Devedor Início mês	Pagamento	Amortização	Juros	Saldo Devedor Final mês
0	$1 000,00	-	-	$10,00	$1 010,00
1	$1 010,00	$210	$200,00	$8,00	$808,00
2	$808,00	$208,00	$200,00	$6,00	$606,00
3	$606,00	$206,00	$200,00	$4,00	$404,00
4	$404,00	$204,00	$200,00	$2,00	$202,00
5	$202,00	$202,00	$200,00	-	-
Total	-	$1 030,00	$1 000,00	$30,00	-

Índice

Inflação

Até agora, consideramos a moeda $ sem inflação. Contudo, a inflação e as variações de preços ocorrem ao longo do tempo e independem da moeda escolhida. A questão reside em como tratar este fenômeno na análise financeira.

A legislação brasileira vigente não permite o reajuste de preços de contratos em intervalos inferiores a 12 meses, mas aceita reajuste de preços em base anual de acordo com índices gerais de preços, tais como IPCA e IGP-M.

Por outro lado, contratos internacionais apresentam cláusulas de reajuste de preço sempre que a inflação ultrapassa determinado valor pré acordado. Este sistema é conhecido como gatilho inflacionário.

Existem duas formas de considerar a inflação na análise financeira; o modelo pós-fixado e o modelo prefixado. Como a inflação futura é desconhecida, sua inclusão nos modelos requer alguns truques.

Modelo Pós-fixado

Neste modelo, considera-se o fluxo de caixa em moeda constante e com taxa de juros sem inflação, conforme as análises anteriores. Para isso, converte-se a moeda do fluxo em moeda indexada de acordo com algum índice escolhido. Contudo, o problema deste método consiste no desconhecimento dos índices inflacionários futuros e, por isso, denomina-se de pós-fixado.

Para contornar este problema, pode-se utilizar uma taxa de inflação estimada para corrigir a taxa nominal de retorno da seguinte maneira²⁸:

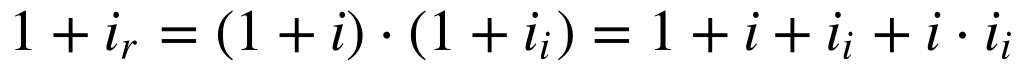
Onde:

• • i_r é a taxa de desconto aparente;
  • i é a taxa de desconto real;
  • i_i é a taxa de inflação.

Observa-se, a partir da equação 20, que para taxas de inflação baixas o produto das taxas pode ser desprezado e a taxa aparente será dada aproximadamente pela soma da taxa real com a taxa da inflação.

---

Exemplos

19. Considere uma aplicação de $ 1 000 em caderneta de poupança rendendo TR mais 0,5 % a.m. Determine a rentabilidade total sabendo que a TR valorizou 0,1771 % a.m. ²⁹

20. Qual a rentabilidade anual desta aplicação? ³⁰

21. Considerando a taxa de inflação anual igual a 9,8% a.a, determine o rendimento real da aplicação anterior.³¹

---

Modelo Pré Fixado

No modelo pré fixado ajustam-se os valores do fluxo de caixa de acordo com a inflação estimada para cada intervalo de tempo e a taxa de juros utilizada deverá ser a aparente, que considera a taxa de inflação.

Índice

Análise de Viabilidade de Projetos

A análise de viabilidade de projetos tem como objetivo escolher projetos e decidir investimentos. Por exemplo:

• • É melhor construir uma hidrelétrica ou uma termelétrica?
  • Qual o financiamento máximo que podemos fazer para um determinado investidor?
  • Dado o valor do investimento necessário para a construção de uma usina, qual deve ser o preço da energia vendida?
  • Dado o preço da energia vendida e o valor do investimento, qual o retorno do projeto?
  • Qual o preço mínimo aceitável num leilão de energia?
  • Qual o preço máximo aceitável num leilão de energia?
  • Qual o impacto do atraso da obra na viabilidade do projeto?
  • Qual a taxa de retorno da fotovoltaica domiciliar?

Para responder a estas e outras perguntas, deve-se detalhar inicialmente o fluxo de caixa do projeto. O fluxo de caixa representa todas as receitas e despesas do projeto durante toda sua vida útil em função do tempo. A partir do fluxo de caixa, realizam-se diversas análises utilizando os conceitos de matemática financeira apresentados anteriormente.

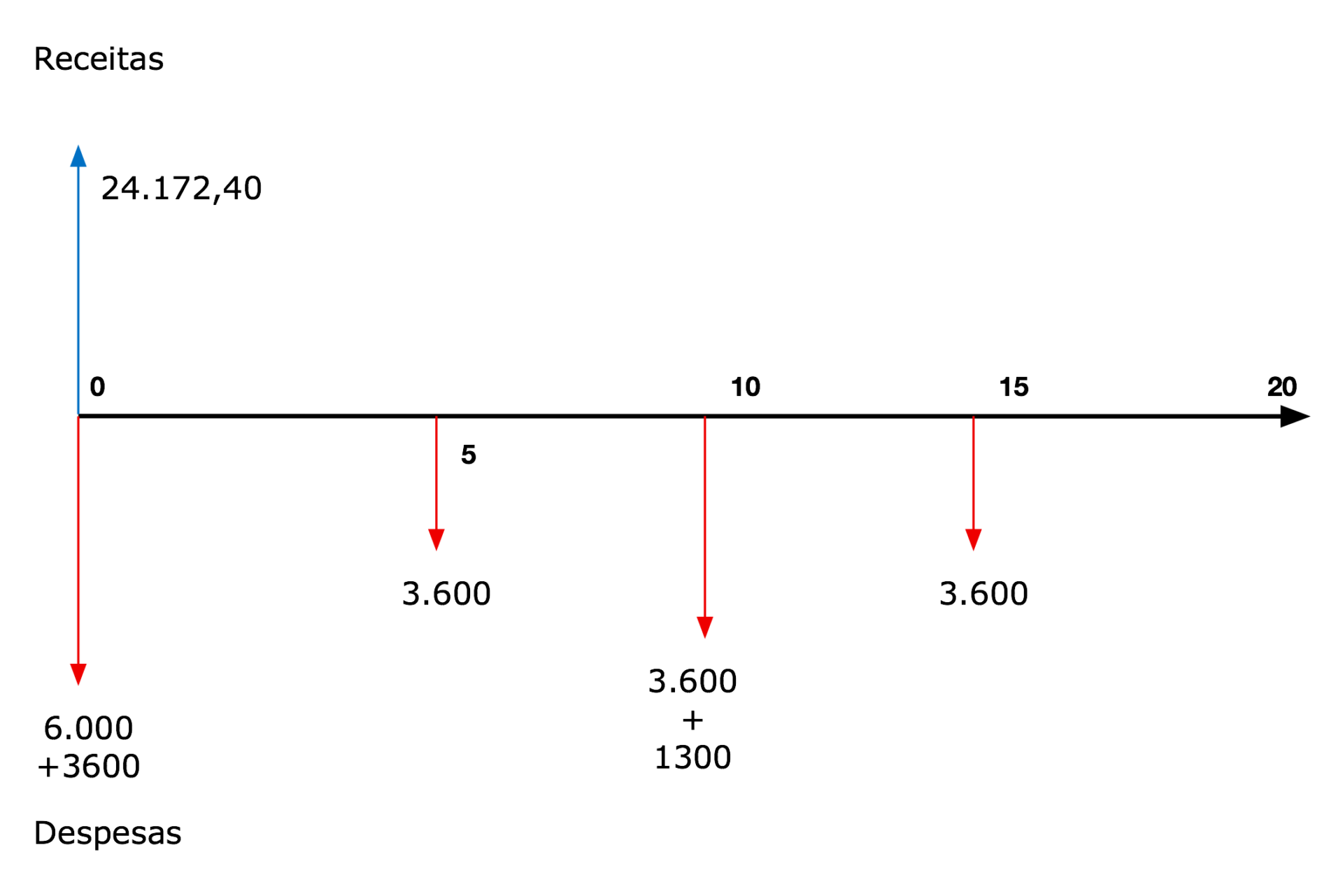
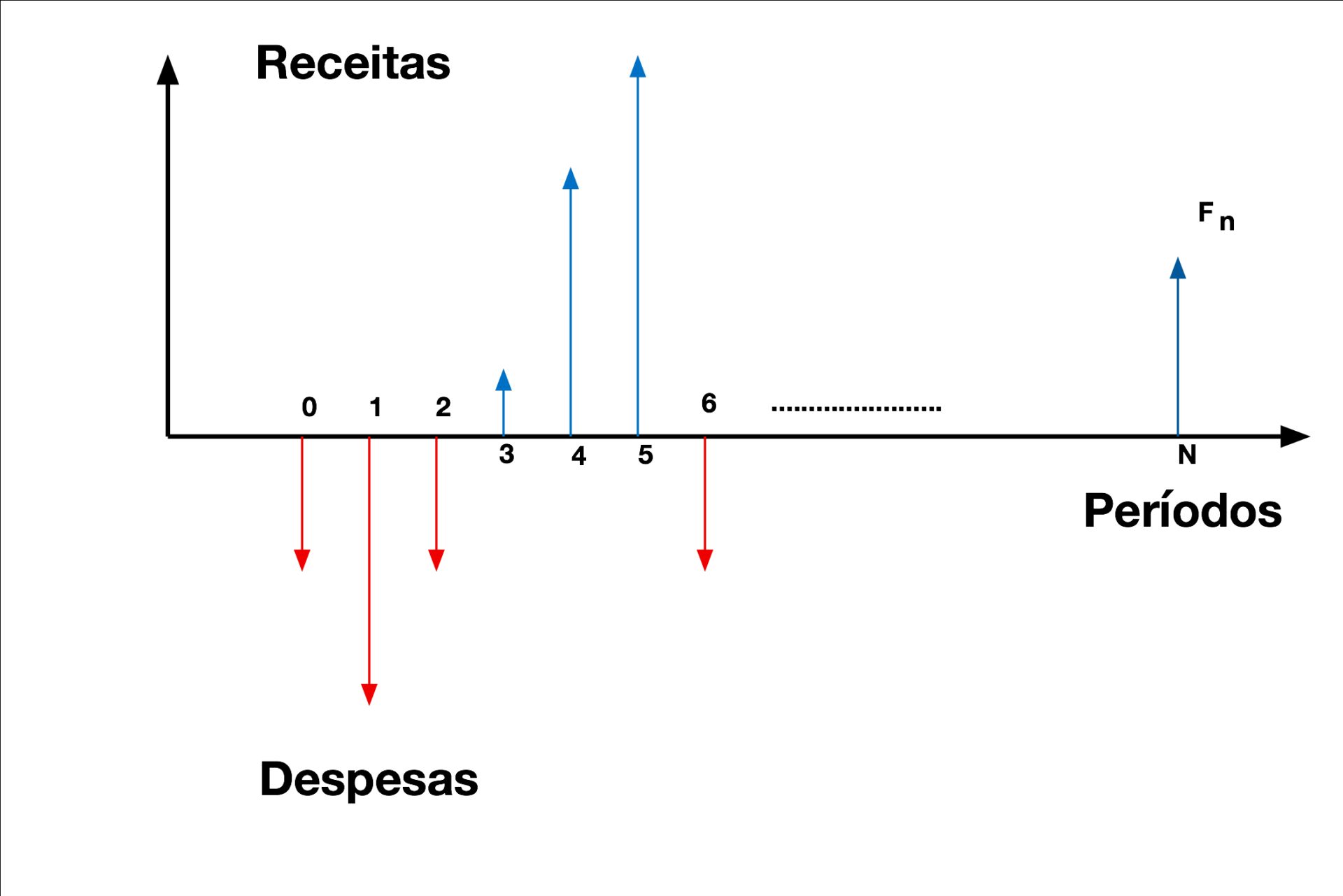
A Figura 5 apresenta o fluxo de caixa de um projeto fictício. Por convenção, despesas aparecem como vetores negativos e receitas como vetores positivos. Quando as receitas ou despesas são iguais, os vetores aparecem como linhas pontilhadas.

---

Exemplo

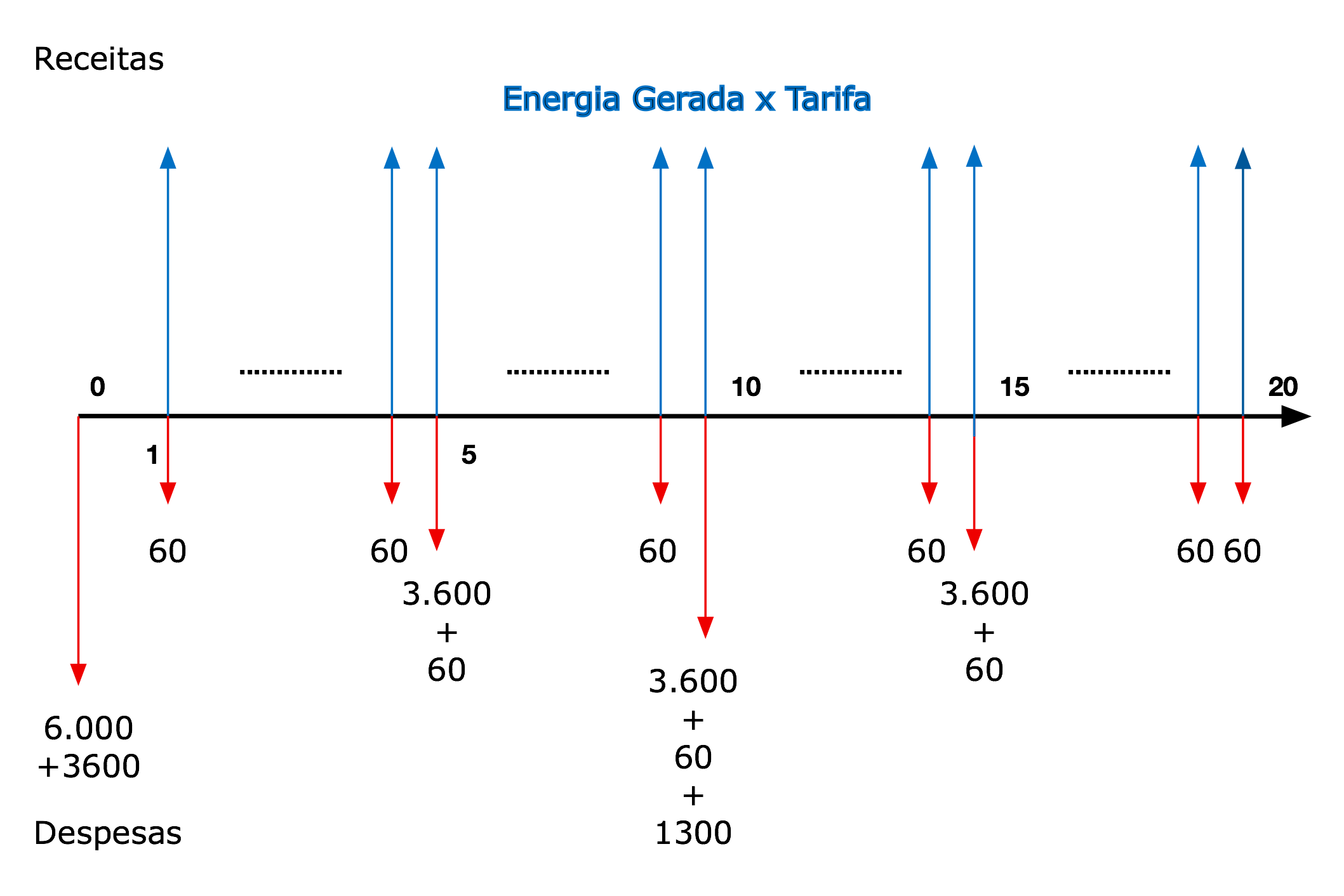
18. Esboce o fluxo de caixa de um projeto de energia solar com as seguintes características:

Projeto Fotovoltaico

Descrição	Valor	Observação
Equipamentos	$ 6.000,00	Investimento inicial
Baterias	$ 3.600,00	Investimento Inicial com troca a cada 5 anos
Troca Inversor	$ 1.300,00	a cada 10 anos
Custo operação e manutenção	$ 60 por ano
Vida útil	20 anos
Taxa de desconto	5% a.a.
Energia Gerada	81 kWh/mês	máxima, 5 horas de sol pleno por dia

Resposta:

Índice

Valor Presente Líquido

---

O Valor Presente Líquido – VPL – de um fluxo de caixa equivale ao valor monetário de todo o fluxo trazido ao instante de tempo inicial do fluxo de caixa. O VPL corresponde à soma das receitas e despesas líquidas do fluxo de caixa descontadas para o instante de referência com uma determinada taxa de desconto. Portanto, o VPL depende da taxa de desconto. Normalmente, como existem diversas receitas e despesas no mesmo período de tempo, a diferença entre receitas e despesas em determinado instante de tempo determina o valor da receita líquida daquele momento. A Equação 21 descreve matematicamente o procedimento de cálculo do VPL.

 

 

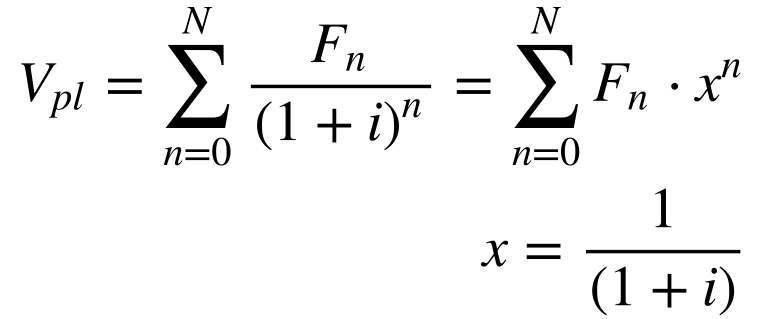
Onde:

• • V_PL é o valor presente líquido [$];
  • F_n é a receita líquida no instante n [$];
  • i é a taxa de desconto;
  • x é uma variável auxiliar;
  • n é o período;
  • N é o número máximo de períodos.

Calcula-se VPL através da equação 21 manualmente com uma calculadora ou digitalmente com uma planilha eletrônica, mas a grande questão consiste na escolha da taxa de desconto.

A taxa de desconto consiste na taxa de retorno desejada pelo investidor. Ela deve ser:

• • maior do que a taxa de juros dos empréstimos bancários;
  • maior do que a maior taxa de retorno dos investimentos de risco equivalente do investidor;
  • maior do que zero;
  • variável e não uma constante determinada pelo governo.

VPLs negativo significam que o projeto não consegue pagar seus custos e tornaram-se inviáveis com a taxa de desconto escolhida.

Por outro lado, VPLs positivos significam que o projeto paga seus custos com alguma folga e possuem viabilidade com a taxa de desconto escolhida.

No caso particular de VPL igual a zero, o projeto encontra-se no limiar da viabilidade porque não agrega nem destrói valor para o investidor.

 

---

Exemplos

22. Considerando a receita anual do exemplo 18 igual a $ 2 000 por ano, determine o VPL do projeto.

Resposta:

Normalmente, utiliza-se uma planilha eletrônica e aplica-se a função financeira de valor presente.³² Porém, neste exemplo, resolveremos manualmente com uma calculadora para fins didáticos. Para facilitar os cálculos, decompomos o fluxo de caixa em partes mais fáceis de calcular. ³³ A arte de resolver este tipo de problema consiste em enxergar como separar o fluxo original no menor número de fluxos de fácil solução.

Primeira parte – Parcela constante do fluxo de caixa

Como a receita e a despesa de O&M³⁴ são constantes ao longo do projeto, podemos utilizar a equação 21 fazendo:

• i=5% ao ano com capitalização anual;
• n=20;

Utilizando estes dados, o valor presente normalizado (V_p/PMT) será igual a 12,46. Como a receita líquida desta parcela é igual a $1 940 (2000-60), o valor presente líquido desta primeira parte é igual a $24 172,40. Desta forma, reduziu-se o fluxo de caixa conforme a figura 6.

Segunda parte – Parcelas únicas

Finalmente, para calcular o valor presente destas três despesas utiliza-se a equação 8, da seguinte maneira:

1. 1. Para cinco anos, teremos um valor presente de -$2 820;
   2. Para dez anos, teremos um valor presente de -$3 008;
   3. Para quinze anos, teremos um valor presente de -$1 732.

Portanto, o valor presente líquido – VPL- deste projeto fica igual a $7 012,40. Contudo, qual o significado deste número? Se compararmos o VPL com o total investido no projeto ($ 21 700), o lucro foi de 32% ao longo de 20 anos. ³⁵ Será que o investidor fez um bom negócio?

23. Suponha que a eficiência do sistema foi inferior ao esperado, que o tempo permanece nublado mais do que previsto, e que, em decorrência desses erros de cálculo, a receita anual ficou reduzida para $ 1 437,00. Qual o novo VPL do projeto? ³⁶

---

A equação 21 não possui solução analítica e isto representa uma limitação na utilização do V_PL. Porém, considerando a equação 7 e o fluxo de caixa uma função contínua no tempo, o V_pl pode ser escrito da seguinte maneira:

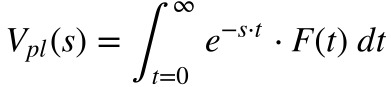
Onde:

• • s é a taxa de desconto de capitalização contínua;
  • V_pl(s) o valor presente líquido em função da taxa de retorno s.

Observa-se que a função V_pl(s) é a transformada de Laplace do fluxo de caixa, e as todas as propriedades desta transformada aplicam-se ao valor presente líquido.

---

Exemplos

24. Determine o valor presente de um fluxo de caixa constante e infinito.

Considerando o valor de uma série geométrica infinita igual a;

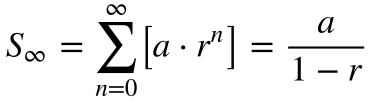e aplicando na equação 21, o valor presente líquido será igual a:

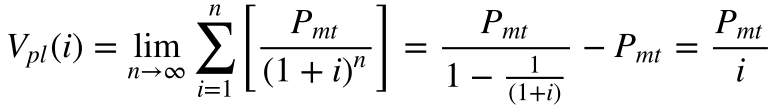A utilização da transformada de Laplace da função constante³⁷ permite obter diretamente o mesmo resultado, conforme a equação abaixo.

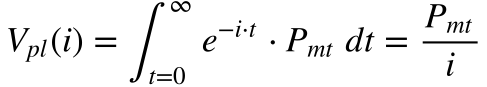25. Determine o efeito do atraso de n anos no início dos pagamentos no valor presente líquido de uma perpetuidade.

Utilizando a transformada de Laplace de um degrau atrasado³⁸, teremos que:

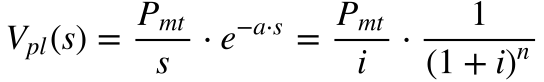
Onde:

• • s é a taxa de desconto com capitalização contínua;
  • i é a taxa de desconto com capitalização discreta;
  • n é o número de anos de atraso.

Este exemplo serve para esclarecer que a taxa de desconto discreta (i) somente se iguala à taxa contínua (s) no caso da perpetuidade. Isto ocorre porque a taxa discreta tende para a taxa contínua quando o número de períodos tende para infinito. Por isso, a equação abaixo fornece relação de conversão entre a taxa contínua (s), utilizada na transformada de Laplace, e a taxa discreta i para os outros casos em que esta hipótese não se aplica.

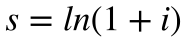
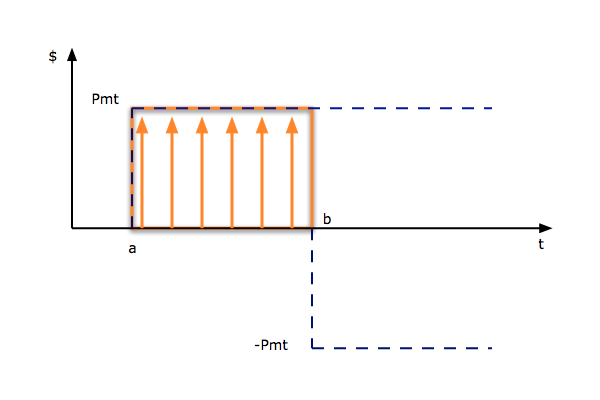
26. Determine o Valor Presente Líquido de uma série de pagamentos constantes com duração finita.

Conforme a figura abaixo, o fluxo de caixa discreto pode ser representado pela diferença de dois fluxos de pagamentos perpétuos defasados no tempo.

A transformada de Laplace da função no tempo da figura 7 será dada, de acordo com JEFFREY, por:

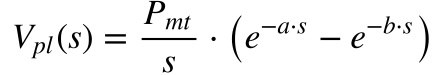
Aplicando as considerações do exemplo anterior na equação 25, o valor presente em função da taxa de desconto discreta será dado por:

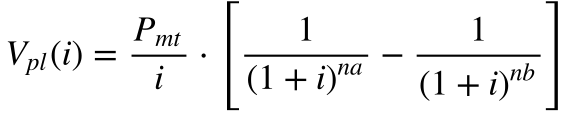
Onde:

• • na é o número de períodos de capitalização referentes ao tempo a;
  • nb é o número de períodos de capitalização referentes ao tempo b.

Demonstre que as equações 26 e 12 se igualam quando o tempo inicial (a) é zero.

---

Os exemplos anteriores mostraram, conforme era de se esperar, que os resultados obtidos com a utilização da Transformada de Laplace são equivalentes aos resultados encontrados com a matemática financeira convencional.

Contudo, a Transformada de Laplace permite resolver de forma mais simples problemas complicados para a matemática financeira convencional.

---

Exemplos

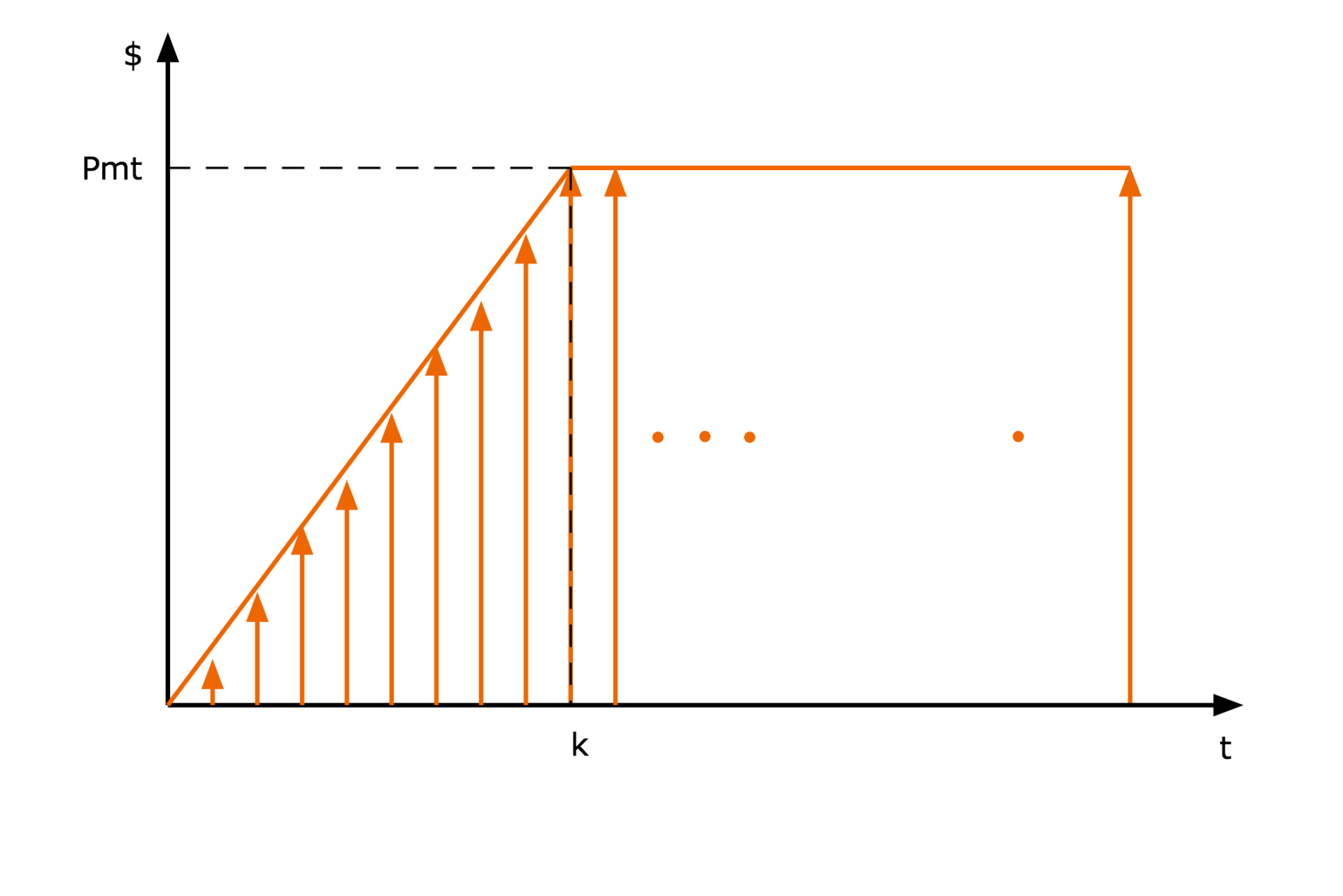
27. Projetos de geração de energia entram em operação de forma escalonada no tempo. Isto acarreta a venda crescente de energia ao longo do início do projeto, e este aumento afeta o valor presente líquido do empreendimento. Portanto, determine o valor presente líquido do fluxo de caixa da figura abaixo, que representa a receita com a venda de energia deste tipo de projeto.

O valor presente líquido do fluxo de caixa da Figura 8, utilizando a Transformada de Laplace, será dado por:

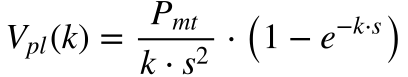
No caso de capitalização discreta, o valor presente líquido ficará igual a:

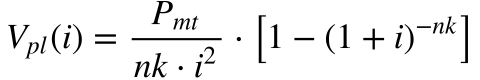
Onde:

• P_mt é o pagamento constante;
• k é o tempo a partir do qual o pagamento fica constante;
• s é a taxa de desconto com capitalização contínua;
• nk é o período de tempo a partir do qual o pagamento fica constante;
• i é a taxa de desconto com capitalização discreta.

Índice

 Taxa Interna de Retorno

O valor presente líquido permite analisar diversos projetos, mas depende da taxa de desconto escolhida. Por isso, criou-se o conceito de Taxa Interna de Retorno-TIR, que representa ³⁹ a taxa de desconto que anula o valor presente do fluxo de caixa. Portanto, a taxa interna de retorno representa a taxa de desconto limítrofe entre lucro e perda. Ou seja, para determinado fluxo de caixa e com esta taxa de desconto, a receita líquida do projeto permite apenas o pagamento do investimento.

A resolução da equação abaixo fornece o valor da TIR.

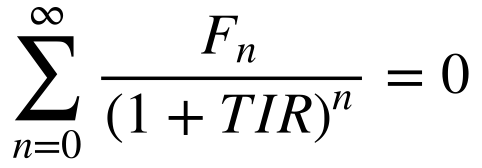
Onde:

• • F_n é o fluxo de caixa no período n;
  • TIR é a taxa interna de retorno;
  • n é o período.

Infelizmente, esta equação não possui solução analítica e sua solução requer também técnicas de cálculo numérico. Contudo, as modernas máquinas de calcular e planilhas eletrônicas⁴⁰ permitem resolver esta questão rapidamente.

---

Exemplos

24. Qual a taxa interna de retorno do exemplo 18? ⁴¹

Índice

---

Tempo de Retorno

O tempo de retorno⁴² é o número de períodos necessário para que o valor presente do fluxo de caixa até aquele período seja igual ao investimento. Isto pode ser escrito da seguinte maneira:

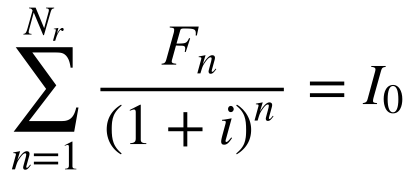
Onde:

• • N_r é o período/tempo de retorno;
  • i é a taxa de desconto;
  • I_o é o investimento inicial.

A equação 24 é semelhante à equação 23, mas a incógnita representa a única diferença. Isto significa que os métodos números utilizados no cálculo da TIR também podem ser utilizados no cálculo do tempo de retorno. Contudo, para fugir do cálculo numérico, considera-se a taxa de desconto igual a zero. Este resultado equivale ao menor tempo de retorno possível deste fluxo de caixa, e quanto maior a taxa de desconto maior o tempo de retorno.

Este indicador apresenta os seguintes problemas:

1. 1. Não considera todo o fluxo de caixa porque o cálculo termina no período de retorno.
   2. Assim como no caso da taxa interna de retorno, existe a possibilidade de diversas soluções para o problema.

Por tudo isso, evita-se utilizar este método na análise de projetos de elevado investimento e de longo prazo.

Índice

 

Bibliografia

1. PUCCINI, A.L., Matemática Financeira Objetiva e Aplicada, Editora Saraiva, 1999.
2. BUSER, S.A., LaPlace Transforms as Present Value Rules: A Note, The Journal of Finance, Vol. XLI, n.1, março de 1986.
3. MURRAY, R. S., LIPSCHUTZ, S., LIU, J., Mathematical Handbook of Formulas and Tables, McGraw-Hill, 2009.
4. JEFFREY,A., DAI, H.H., Handobook of Mathematical Formulas and Integrals, 4 edição, Elsevier, 2008.

Voltar ao Início