A maior dificuldade prática da Equação de Schrödinger reside na dificuldade de resolução de sistemas com muitas partúiculas. Por isso, utilizam-se diversas simplificações para analisar sistemas complexos. A partícula na caixa representa uma dessas simplificações.
Para visualizar melhor o significado e implicações da Equação de Schrödinger, considera-se o exemplo de uma partícula em movimento unidimensional dentro de uma caixa – Fig. 1.
Nesse caso, para manter uma partícula eletricamente carregada confinada entre os pontos 0 e a, torna-se necessário criar uma barreira de potencial elétrico infinito nas fronteiras com polaridade contrária à da carga.

Matematicamente, isto requer as seguintes condições de contorno:
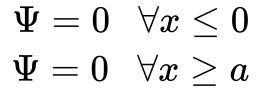
Este exemplo transforma a Equação 6 do Capítulo Equação de Schrödinger na seguinte equação diferencial. 1
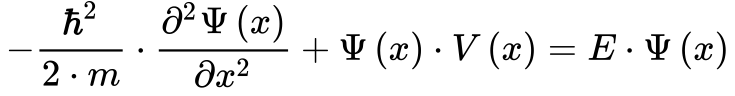
Como o potencial dentro da caixa é zero, a Equação 2 se transforma em2:
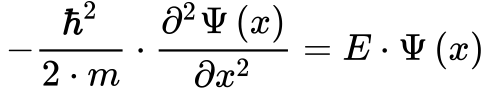
A Equação 4 fornece a solução geral da Equação 3
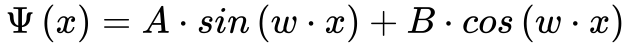
Aplicando as condições de contorno, apresentadas na Equação 1, na Equação 4, obtem-se a seguinte expressão:
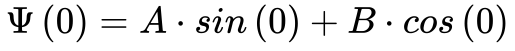
A solução da Eq. 5 requer que B seja sempre igual a zero e:
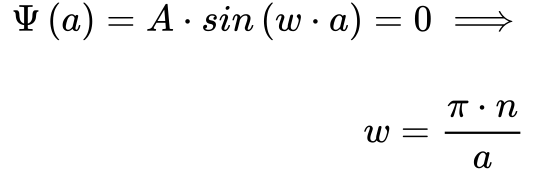
A Equação 6 demonstra que existem n soluções dadas pela Equação 7, e que n deve ser um número inteiro maior do que zero. A constante An pode ser um número real ou complexo.
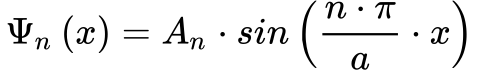
Substituindo a Equação 7 na Equação 3, obtem-se a energia cinética da partícula:
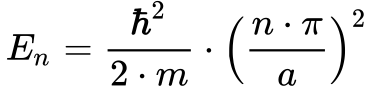
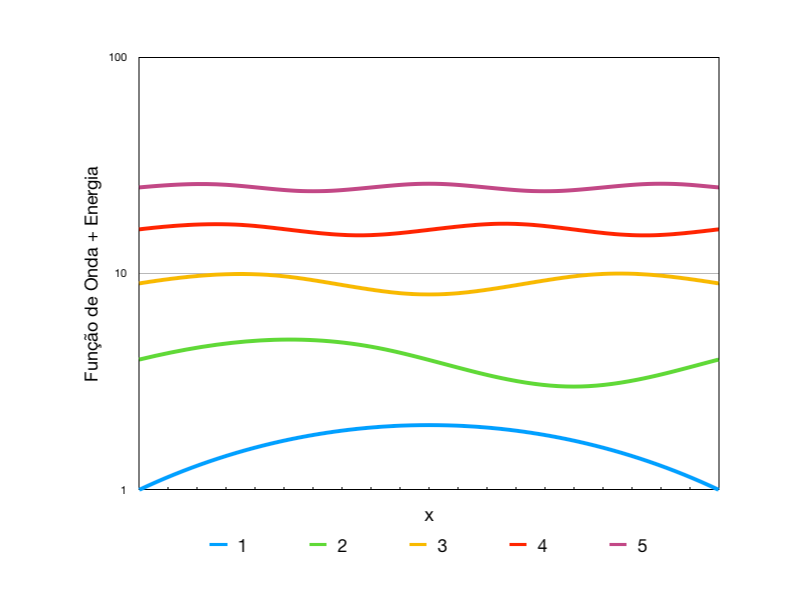
A matemática revelou o comportamento quântico da partícula. A Figura 2 mostra as n soluções possíveis com níveis de energia e funções de onda distintos.
Finalmente, resta normalizar as funções de onda. Para isso precisamos calcular a integral do módulo da função de onda ao quadrado3 conforme a equação abaixo:
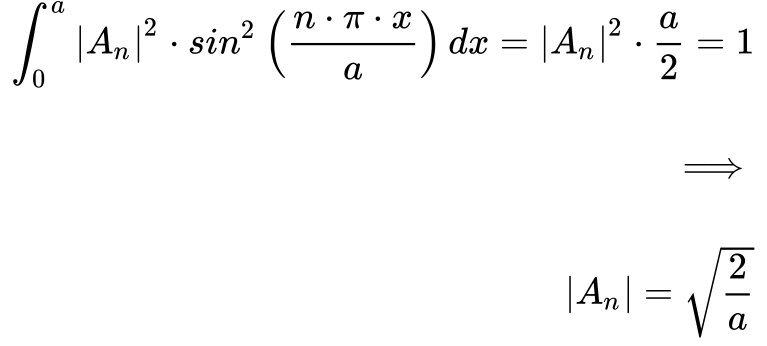
Portanto, a normalização requer que o valor das amplitudes da onda para que a integral da Equação 9 seja unitário.
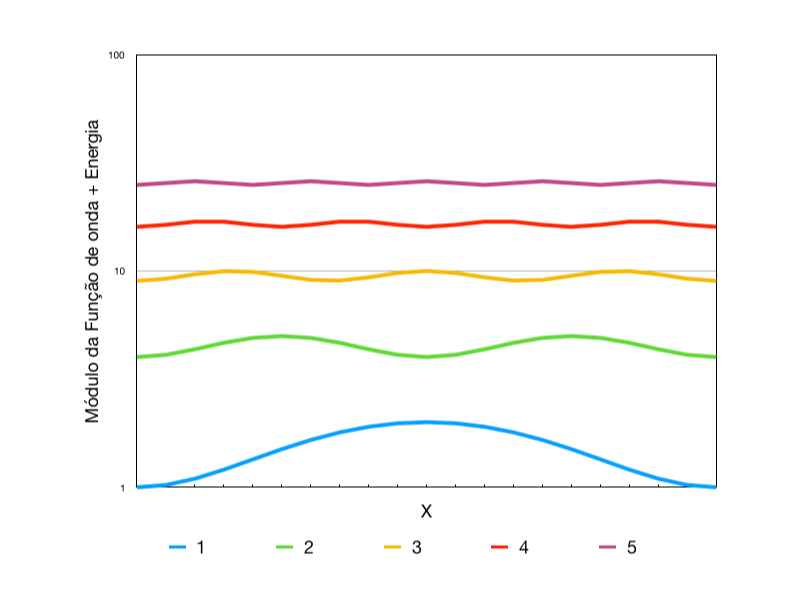
Finalmente, a Figura 3 apresenta o módulo da função de onda elevada ao quadrado e, neste caso, somada à energia de cada nível. Considerando que este gráfico representa a probabilidade de localização da partícula dentro caixa, observamos que:
-
- a probabilidade é mínima de encontrar elétrons nas bordas da caixa4;
- a probabilidade de encontrar elétrons no centro da caixa é máxima apenas para números quânticos ímpares;
- Com o aumento do nível energético, surgem outros pontos de máxima e de mínima probabilidade;
- Para números quânticos pares o centro passa a apresentar probabilidade mínima e nos ímpares máximas;
Este exemplo simples revelou aspectos importantes da mecânica quântica.
-
- A energia assume apenas um conjunto de valores discretos;
- Existe um valor mínimo de energia para a partícula, superior ao valor mínimo do poço;
- O módulo da função de onda ao quadrado revela que a partícula não permanece uniformemente distribuída na caixa e que essa distribuição depende do número quântico e, consequentemente da energia.
- Estes comportamentos inexistem se considerarmos a mecânica clássica aplicada a uma mesa de bilhar.
Referências
- KREYSZIG, E. Advanced Engineering Mathematics, 9 edição, John Wiley & Sons, 2006.
- SOLYMAR, L., WALSH, D., Electrical Properties of Materials, Oxford, 2010.
- MILLER, D.A.B, Quantum Mechanics for Scientists and Engineers, Cambridge University Press, 2008.