Simetria constitui um importante conceito que envolve o desenho, as artes, os materiais, a matemática, e a física. Neste capítulo, estaremos interessados nos aspectos da simetria aplicados aos materiais.
Grupos
A Teoria de Grupos fornece os conceitos matemáticos necessários para o estudo da Simetria aplicada à Ciência dos Materiais.
Grupos consistem em conjuntos de Elementos sujeitos a determinados critérios e que se relacionam de acordo com regras específicas denominadas Operações – *. Define-se Ordem do Grupo como sendo número de Elementos1 do Grupo e existem as seguintes propriedades para que um conjunto possa formar um Grupo:
-
- A operação de dois elementos de um Grupo sempre gera outro elemento pertencente ao Grupo2;
- As Operações do Grupo são distintas, isto é, nenhum par de operações produz os mesmos resultados em todos os casos.3
- O resultado da aplicação de sucessivas operações em elementos do grupo constitui outra operação do grupo.
- Existe um Elemento do Grupo, denominado de Unitário ou Identidade – E, que obedece à Equação 1;
- Todo Elemento pertencente ao Grupo possui um outro Elemento Recíproco -R – ou Inverso -I, que também pertence ao Grupo, conforme a Equação 2.
- As Operações do Grupo são Associativas conforme a Equação 3. Contudo, não precisam ser comutativas. Grupos que também possuem a propriedade associativa denominam-se Grupos Abelianos.
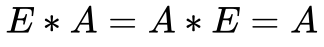
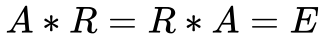
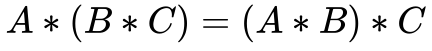
Os Grupos podem possuir um número de Elementos e Operações finito ou infinito.
Grupos Espaciais representam um caso particular de Grupos de Transformação de Coordenadas que preservam o comprimento4.
A Equação 4 representa uma transformação de coordenadas linear genérica.
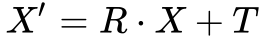
Onde:
-
- X’ é o vetor das novas coordenadas;
- R é a matriz de transformação;
- X é o vetor das antigas coordenadas;
- T é o vetor de translação.
Para que a transformação da Equação 4 preserve o comprimento, a matriz R e o vetor T devem ser reais e a matriz R ortogonal5 e o vetor T também deve ser real.
Toda matriz ortogonal pode ser escrita da seguinte maneira após a transformação unitária com outra matriz ortogonal:
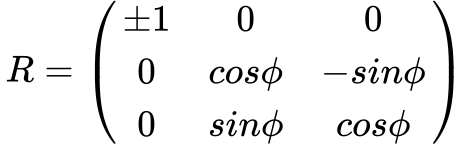
Geometricamente, esta matriz representa uma transformação de coordenadas onde x1 se mantém constante6
Existem dois conceitos básicos na Teoria de Grupos:
-
- Elementos;
- Operações.
Os Elementos consistem no conjunto de objetos matemáticos nos quais as operações podem ser aplicadas.
Normalmente, mais de uma operação pode ser aplicada num mesmo elemento. Por exemplo, as rotações de qualquer múltiplo inteiro de 90 graus num cubo produz um elemento indistinguível do original.
Operações são funções matemáticas que transformam geometricamente os elementos num elemento indistinguível do original. Por exemplo, a rotação de 90 graus de um cubo produz outro cubo absolutamente igual ao cubo original.
O Elemento consiste no objeto geométrico, ponto, linha, plano, ou figura no qual a operação é aplicada. Normalmente, mais de uma operação pode ser aplicada num mesmo elemento. Por exemplo, as rotações de qualquer múltiplo inteiro de 90 graus num cubo produz um elemento indistinguível do original.
As operações de simetria relativos a objetos macroscópicos são:
-
- Identidade – E;
- Espelhamento plano – m;
- Simetria Rotacional – n= 2,3,4,6;
- Centro de Inversão – i ou ‾1;
- Eixo de rotoinversão – ‾3.
Identidade -E
A Identidade existe para todos os objetos, mesmo os assimétricos, porque todos equivalem a eles mesmos. Por exemplo, a rotação de qualquer objeto de 360 graus produz outro elemento idêntico. O conceito de Identidade constitui um conceito fundamental da matemática, que estabelece que x,y,z = x,y,z.
Espelhamento Plano- m
Espelhamento plano, reflexão plana, simetria especular, ou simetria de reflexão ocorre quando a sua imagem num espelho plano permanece idêntica à original. Matematicamente, a transformação y’=y, z’=z, x’=-x representa a reflexão em relação ao plano yz.
Se voltarmos ao exemplo do papel de parede – Figura 1 – observamos que planos verticais, horizontais e com inclinações de ± 45 graus funcionam com espelhos para esta figura.

A Figura 2 apresenta outros exemplos de Espelhamento Plano. Observa-se que o número de Elementos depende da simetria da figura, e o círculo/esfera possui infinitos Elementos.
Os planos que dividem os Triângulos em dois triângulos retângulos realizam espelhamento plano, assim como os planos ortogonais no quadrado. O mesmo ocorre com os planos defasados de 120 graus no Hexágono.
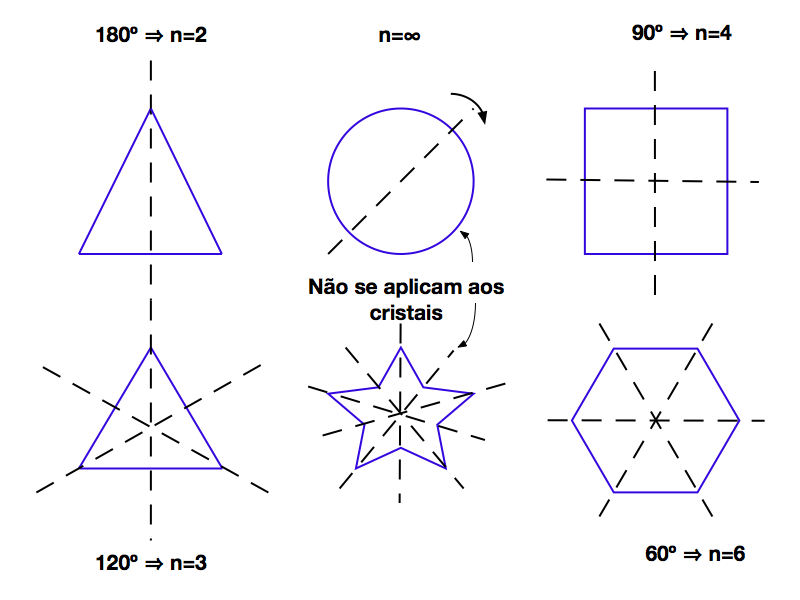
Simetria Rotacional- n
A simetria rotacional existe quanto a rotação da figura de determinados ângulos a deixa indistinguível, e convencionou-se designar a rotação por n quando o ângulo de rotação for 360° ÷n. A Figura 2 exemplifica também este elemento. Por exemplo, o triângulo isósceles apresenta uma simetria rotacional de 2, e assim por diante.
É importante apontar que a Simetria Rotacional pode existir simultaneamente, ou não, com Espelhamento Plano. Porém, qualquer par de Planos de Espelhamento ortogonais geram uma Simetria Rotacional de ordem 2.
Contudo, no caso específico da Cristalografia, apenas existem os casos de Simetria Rotacional 2,3,4 e 6. Contudo, existem simetrias de ordem 5,7, etc, em algumas moléculas isoladas, e alguns agregados sólidos podem apresentar Simetria Rotacional de ordem 57.
Centro de Inversão – i
O Centro de Inversão, origem de simetria ou ponto de simetria consiste no ponto cuja distância às outras partes similares da figura se mantêm constante. Por exemplo, no caso do papel de parede, os centros das duas figuras são pontos de simetria. Matematicamente, se definirmos o Centro de Inversão como a origem do sistema de coordenadas, teremos que todo ponto x,y,z será indistinguível do ponto -x,-y,-z. Outra forma de visualizar este conceito consiste em imaginar o Centro de Inversão como um espelho pontual que reflete todos os pontos da forma geométrica.
Para ilustrar melhor, a Figura 3 compara o Espelhamento Plano com o Centro de Inversão para uma mesma figura.
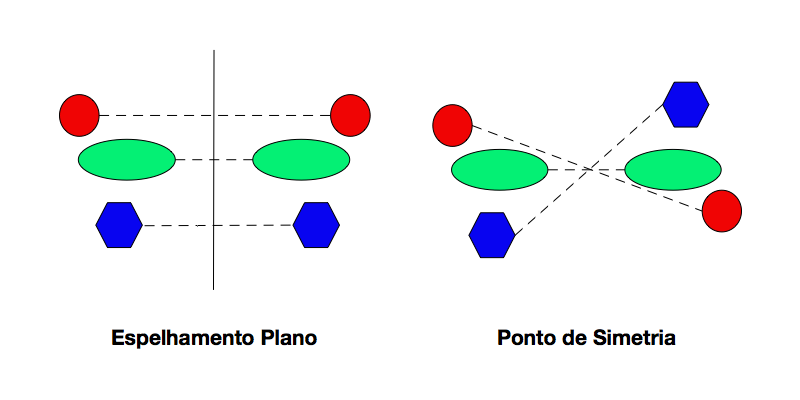
Rotoinversão – ‾n
A Rotoinversão consiste de dois elementos aplicados em sequência; uma Simetria Rotacional 360º/n seguida por um Centro de Inversão, localizada no eixo de Rotoinversão. A realização de duas operações em sequência pode ou não gerar uma nova simetria.
Por exemplo, a Figura 3 apresenta a Rotoinversão de n=1 para um ponto8. Inicialmente existe uma rotação de 360 graus e, em seguida uma Centro Inversão com relação ao ponto de simetria. Observa-se que este resultado equivale a um Centro Inversão simples porque a rotação de 360 equivale a uma Identidade. Por isso, a Rotoinversão n=1 não constitui uma nova simetria.
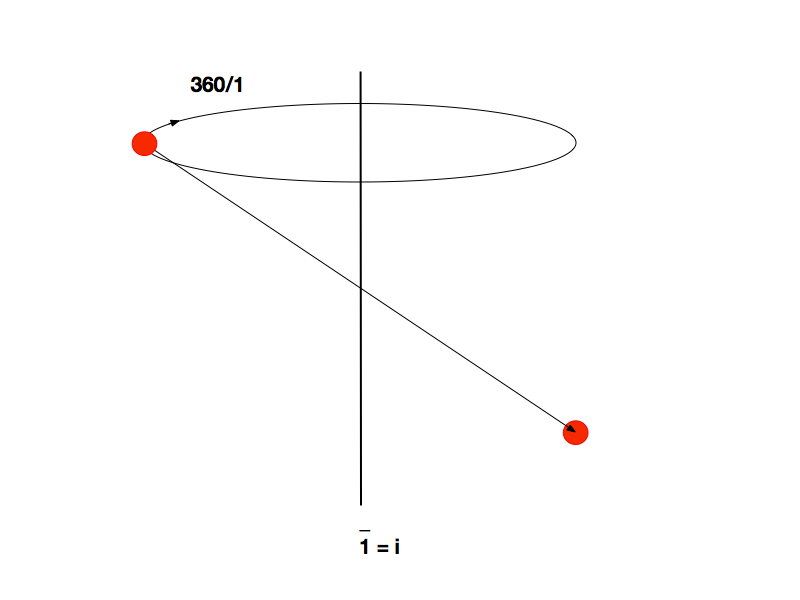
Analogamente, a Figura 4 apresenta a Rotoinversão para n=2, que equivale ao Espelhamento Plano. Também , neste caso, a Rotoinversão n=2 não representa uma nova simetria.
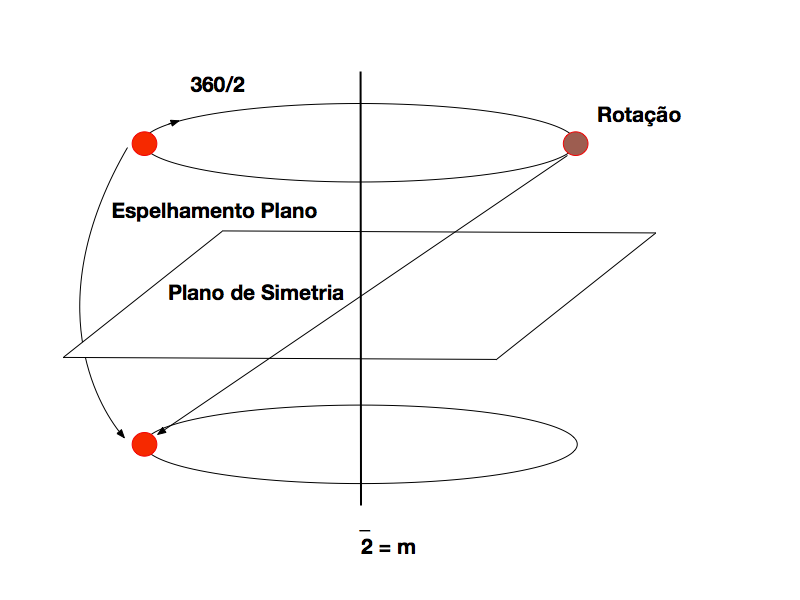
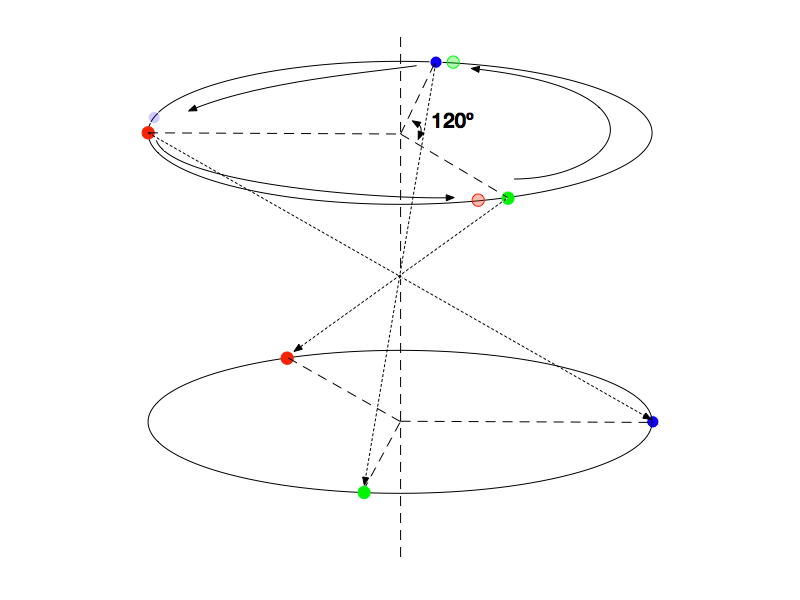
A Figura 5. mostra a Rotinversão n=3, uma rotação de 120 graus seguida de uma ponto inversão. Neste caso obtemos uma nova simetria.
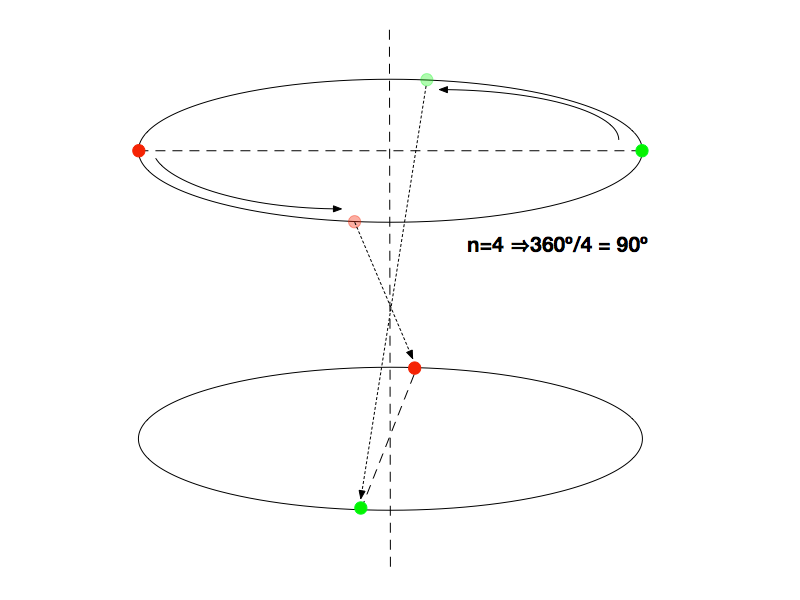
A Figura 6 apresenta a Rotoinversão n=4, que consiste numa rotação de 90º seguida de uma ponto inversão, configurando também uma nova simetria.
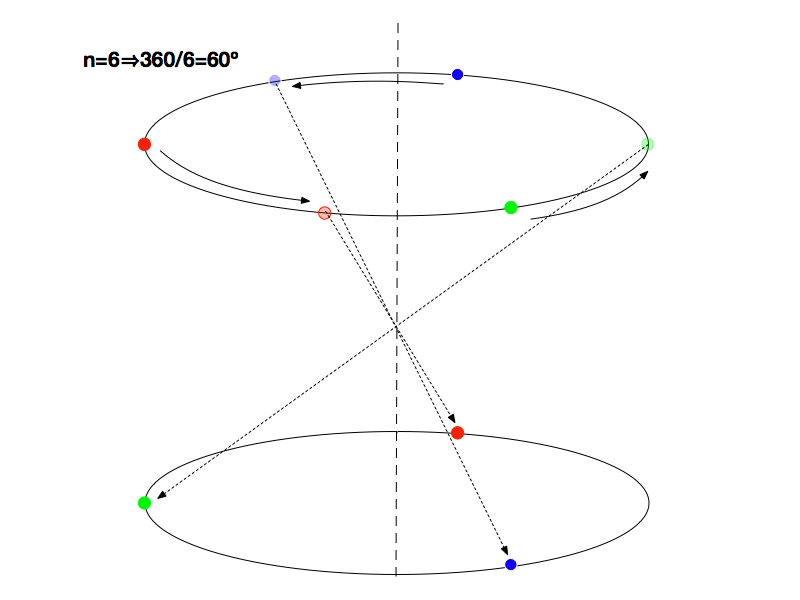
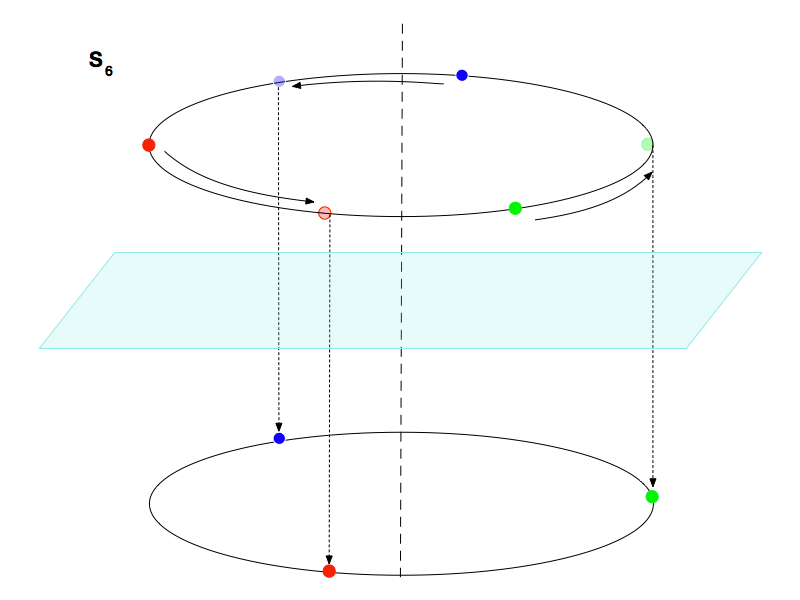
Finalmente, chegamos na última Rotoinversão possível em cristais – n = 6, que consiste num rotação de 60º seguida de uma ponto inversão, conforme mostra a Figura 7.
Historicamente, a Cristalografia se desenvolveu paralelamente à química apesar dos conceitos de simetria serem conceitos matemáticos únicos.
Carl Hermann, cristalografista alemão desenvolveu com Charles Mauguin, mineralogista francês, a notação cristalográfica, denominada Hermann-Mauguin, aceita internacionalmente a partir de 1935 e utilizada no capítulo Simetrias
Contudo Arthur Schoenflies, matemático alemão, desenvolveu outra notação, denominada notação Schoenflies, muito utilizada no estudo das simetria molecular.
A Tabela 1, que apresenta os dois sistemas, mostra que ambos possuem os mesmos elementos, que possuem símbolos diferentes, mas os últimos elementos possuem pequenas distinções.
Tabela 1.Sistemas de Simetria
wdt_ID Elemento (S) Schoenflies Elemento(HM) Hermann-Mauguin
1
Identidade
E
Identidade
1
2
Espelhamento Plano
σ
Espelhamento Plano
m
3
Simetria Rotacional
Cn
Simetria Rotacional
n
4
Centro de Inversão
i
Centro de Inversão
‾1
5
Rotoreflexão
Sn
Rotoinversão
‾n
Rotoreflexão
A Rotoreflexão consiste numa simetria Rotacional seguida de uma Reflexão num plano.
A Figura 8 apresenta a rotoreflexão de ordem 1, que é exatamente igual à Rotoinversão de ordem 29
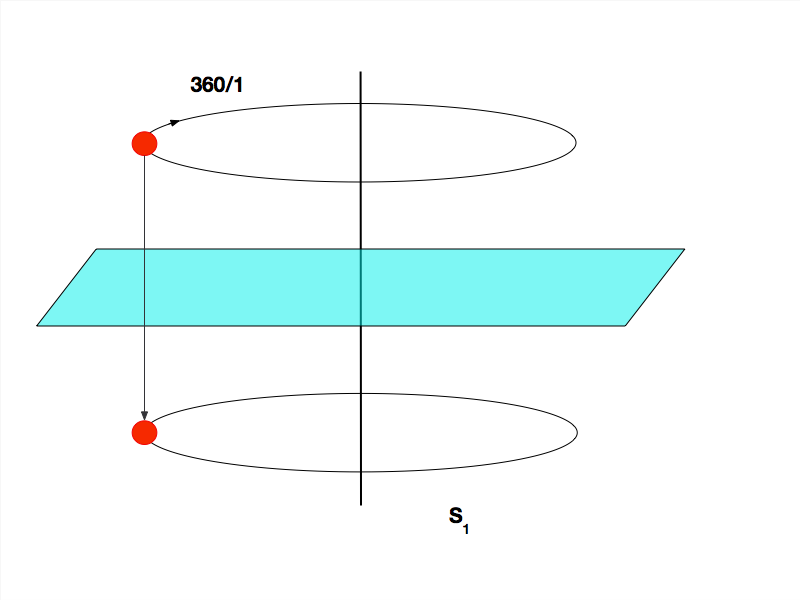
A Figura 9 apresenta a Rotoreflexão de ordem 2, que, por sua vez, é exatamente igual à Rotoinversão de ordem 110.
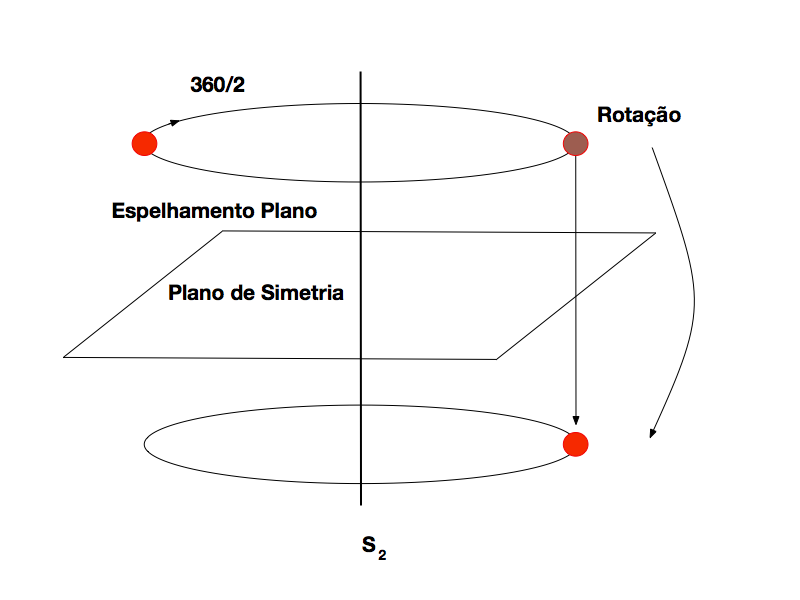
A Figura 10 apresenta a Rotoreflexão de ordem 3, que difere da rotoinversão de ordem 3, mas se confunde com a de ordem 6 no caso dos elementos serem indistinguíveis.
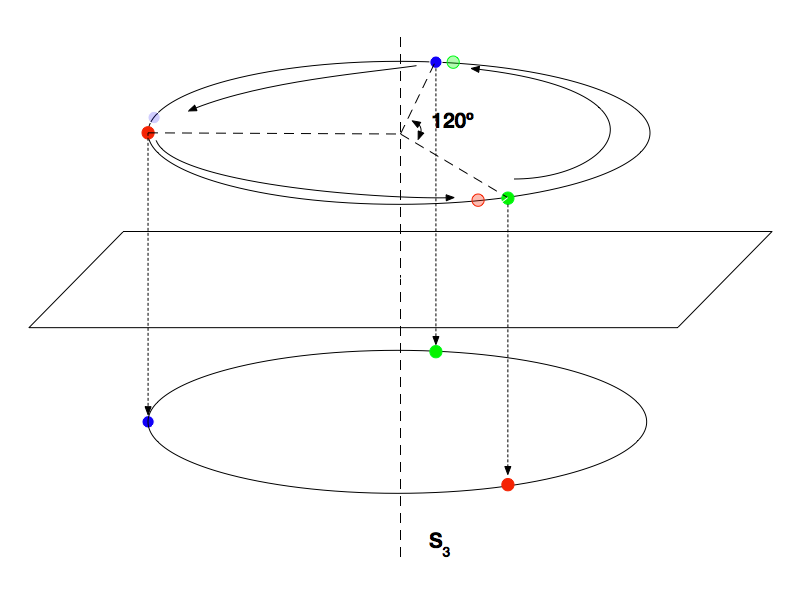
A Figura 11 mostra a Rotoreflexão de ordem 4, que difere da Rotoinversão de mesma ordem, a menos que os elementos sejam iguais.
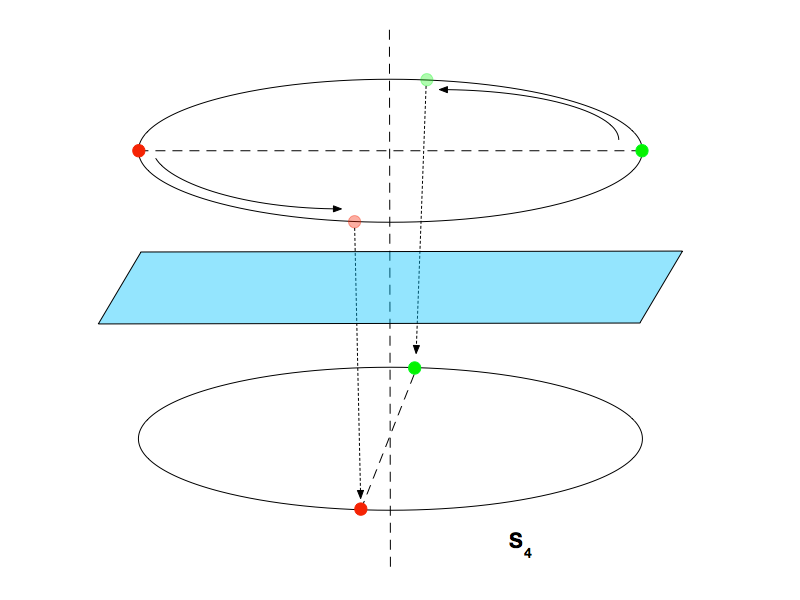
A Figura 12 apresenta a Rotoreflexão de ordem 6, que também difere da rotinversão.
Bibliografia
- BURNSIDE, W., Theory of Groups of Finite Order, Cambridge, 1897.
- KOSTER, G.F., Space Groups and their Representations, Academic Press, 1957.
- PATTERSON, J., BAILEY, B., Introduction to the Theory of Solid-State Physics, Springer, 2 ed., 2010.
- POWELL, R. C., Symmetry, Group Theory, and the Physical Properties of Crystals, Springer, 2010.
- RAMOND P., Group Theory – A Physicist’s Survey, Cambridge, 2010.
